题目内容
若平面向量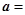
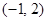 与b的夹角是
与b的夹角是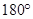 ,且︱
,且︱ ︱
︱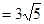 ,则b的坐标为( )
,则b的坐标为( )
A.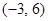 | B. | C.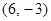 | D. |
B
解析试题分析:设b= ,因为︱
,因为︱ ︱
︱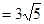 ,所以
,所以 ,又平面向量
,又平面向量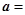
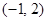 与b的夹角是
与b的夹角是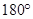 ,所以
,所以 ,联立
,联立 ,解得
,解得 ,所以b的坐标为
,所以b的坐标为 ,选B.
,选B.
考点:平面向量数量积、平面向量的模.

练习册系列答案
相关题目
在 中, AD=3,点P在AD上且满足
中, AD=3,点P在AD上且满足 则
则 ( )
( )
| A.6 | B. | C.-12 | D. |
已知向量 满足:
满足: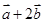 与
与 垂直,且
垂直,且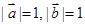 ,则
,则 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
已知非零向量 和
和 满足
满足 ⊥(
⊥( -
- ),
), ⊥(2
⊥(2 -
- ),则
),则 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
已知两点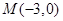 ,
,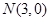 ,点P为坐标平面内一动点,且
,点P为坐标平面内一动点,且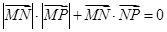 ,则动点
,则动点 到点
到点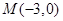 的距离的最小值为( )
的距离的最小值为( )
| A.2 | B.3 | C.4 | D.6 |
已知 是两夹角为120°的单位向量,
是两夹角为120°的单位向量, ,则
,则 等于( )
等于( )
| A.4 | B. | C.3 | D. |
已知向量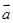 、
、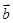 满足
满足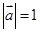 ,
,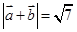 ,
,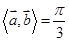 ,则
,则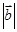 等于 ( )
等于 ( )
A.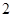 | B. | C.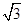 | D.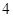 |
已知 均为单位向量,它们的夹角为60°,那么
均为单位向量,它们的夹角为60°,那么 等于 ( )
等于 ( )
A. | B.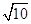 | C. | D.4 |
设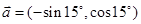 ,则
,则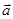 与
与 轴正方向的夹角为( )
轴正方向的夹角为( )
A.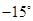 | B.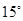 | C.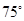 | D.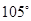 |