题目内容
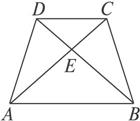
如图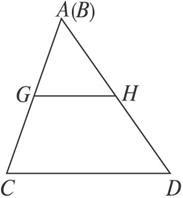
图
探讨GH与AB、CD的关系.
解析:猜想当A、B重合,AC与BC重合,
梯形变为三角形,如图
由三角形中位线定理知GH=![]() CD.
CD.
一般地,GH肯定与AB有关,可能GH=![]() (CD+AB)或GH=
(CD+AB)或GH=![]() (CD-AB).
(CD-AB).
通过观察,GH不大于![]() CD,所以猜想GH=
CD,所以猜想GH=![]() (CD-AB).
(CD-AB).
下面给出证明.
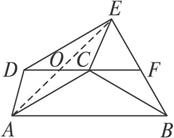
证明:如图

图
连结AH并延长交CD于E.
∵AB∥CD,∴∠ABH=∠EDH,BH=DH,
∠AHB=∠EHD.
∴△ABH≌△EDH.
∴AH=EH,AB=ED.
又∵AG=CG,∴GH=![]() CE
CE
=![]() (CD-ED)
(CD-ED)
=![]() (CD-AB).
(CD-AB).

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目