Question

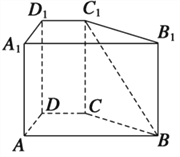
【题目】半径为2的球O内有一内接正四棱柱（底面是正方形，侧棱垂直底面），当该正四棱柱的侧面积最大时，球的表面积与该四棱柱的侧面积之差是 ．

Answer 1

【答案】16π﹣16
【解析】解：设正四棱柱的底面边长为a，高为h，则2a2+h2=16≥2 ah，
∴ah≤4 ，当且仅当h= a= 时取等号，
∴正四棱柱的侧面积S=4ah≤16 ，
∴该正四棱柱的侧面积最大时，h=2 ，a=2，
∴球的表面积与该四棱柱的侧面积之差是4π22﹣16 =16π﹣16 ．
所以答案是：16π﹣16 ．
【考点精析】解答此题的关键在于理解球内接多面体的相关知识，掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长．