题目内容
已知F1、F2分别是椭圆
＝1(a＞b＞0)的左、右焦点，A、B分别是此椭圆的右顶点和上顶点，P是椭圆上一点，O是坐标原点，OP∥AB，PF1⊥x轴，F1A＝
＋
，则此椭圆的方程是________________．
＝1(a＞b＞0)的左、右焦点，A、B分别是此椭圆的右顶点和上顶点，P是椭圆上一点，O是坐标原点，OP∥AB，PF1⊥x轴，F1A＝＋，则此椭圆的方程是________________．
＝1由于直线AB的斜率为－
，故直线OP的斜率为－，直线OP的方程为y＝－x.与椭圆方程联立得＝1，解得x＝±
a.根据PF1⊥x轴，取x＝－a，从而－a＝－c，即a＝
c.又F1A＝a＋c＝＋，故c＋c＝＋，解得c＝，从而a＝.所以所求的椭圆方程为＝1
，故直线OP的斜率为－，直线OP的方程为y＝－x.与椭圆方程联立得＝1，解得x＝±a.根据PF1⊥x轴，取x＝－a，从而－a＝－c，即a＝c.又F1A＝a＋c＝＋，故c＋c＝＋，解得c＝，从而a＝.所以所求的椭圆方程为＝1
练习册系列答案
阅读快车系列答案
相关题目
：
的离心率为
，右焦点为(
，0)．
作两条互相垂直的射线，与椭圆交于
，
两点，求证：点
的距离为定值.
在椭圆
上,若
点坐标为
,
,且
则
的最小值是（ ）
＝1(m>1)的左焦点为F1.若直线l与椭圆C交于A，B两点，满足
·
＝0，求实数m的值．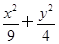
＝1的焦点为F1、F2，点P为椭圆上的动点，当∠F1PF2为钝角时，求点P的横坐标x0的取值范围．
＝1的右顶点，点D(1，0)，点P、B在椭圆上，
＝
.
+
=1上有两个动点P、Q,E(3,0),EP⊥EQ,则
·
的最小值为( )
＝1(a＞b＞0)的两个焦点，P为椭圆C上一点，且
⊥
.若△PF1F2的面积为9，则b＝________.