题目内容
已知函数f(x)=x2-2|x|-3,x∈R
(1)判断f(x)的奇偶性;
(2)画出函数f(x)的图象;
(3)求f(x)的单调增区间.
(1)判断f(x)的奇偶性;
(2)画出函数f(x)的图象;
(3)求f(x)的单调增区间.
考点:函数图象的作法,函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)利用函数的奇偶性的定义即可判断,
(2)去掉绝对值,化为分段函数,绘图即可,
(3)利用图象,直接看出单调区间.
(2)去掉绝对值,化为分段函数,绘图即可,
(3)利用图象,直接看出单调区间.
解答:
 解:(1)∵f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x),
解:(1)∵f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x),
∴f(x)为偶函数,
(2)∵f(x)=x2-2|x|-3=
,
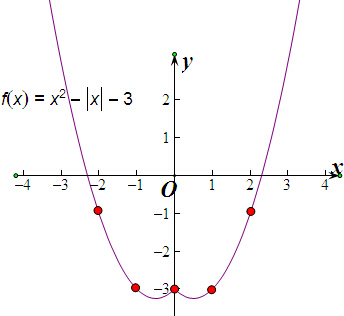
图象如图所示,
(3)由图象可以看出,f(x)的单调在增区间为(-
,0)和(
,+∞)
 解:(1)∵f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x),
解:(1)∵f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x),∴f(x)为偶函数,
(2)∵f(x)=x2-2|x|-3=
|
图象如图所示,
(3)由图象可以看出,f(x)的单调在增区间为(-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了函数的奇偶性和单调性以及含有绝对值函数的图象的画法,属于基础题.

练习册系列答案
相关题目

 (文科)已知二元一次不等式组
(文科)已知二元一次不等式组