题目内容
经过曲线C：
(
为参数)的中心作直线l:
（t为参数）的垂线，求中心到垂足的距离.
(为参数)的中心作直线l:（t为参数）的垂线，求中心到垂足的距离.中心到垂足的距离为
由曲线C的参数方程
消去参数，
得(x-3)2+y2=9.
曲线C表示以（3，0）为圆心，3为半径的圆.
由直线l的参数方程,
消去参数t,得y=
x.
表示经过原点，倾斜角为30°的直线.
如图,在直角三角形OCD中，OC=3，∠COD=30°，
所以CD=.所以中心到垂足的距离为.
消去参数，得(x-3)2+y2=9.
曲线C表示以（3，0）为圆心，3为半径的圆.
由直线l的参数方程
,消去参数t,得y=
x.表示经过原点，倾斜角为30°的直线.
如图,在直角三角形OCD中，OC=3，∠COD=30°，
所以CD=
.所以中心到垂足的距离为.
练习册系列答案
口算能手系列答案
相关题目
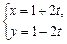（t为参数）被圆
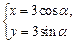（α为参数）截得的弦长．
，曲线C的参数方程为
．
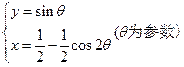与直线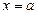
有两个不同的公共点，则实数
的取值范围是_________________.
上的两点
对应的参数分别为
，
，那么
=_______________。
（
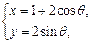为参数）化成普通
方程为 ．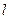
的参数方程是
（
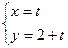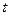是参数），以原点
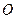为极点，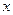
轴正半轴为极轴建立极坐标系，圆
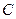的极坐标方程为
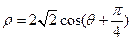，则圆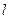
的距离是 .