题目内容
4.sin10°cos20°+cos10°sin20°=$\frac{1}{2}$.分析 直接根据两角和的正弦公式计算即可.
解答 解:sin10°cos20°+cos10°sin20°=sin30°=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 本题考查的知识点是两角和的正弦公式,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15.若变量x,y满足$\left\{\begin{array}{l}{2x+y-5≥0}\\{x-y+5≥0}\\{2x-y-5≤0}\end{array}\right.$ 则x2+y2的最小值为( )
| A. | $\frac{25}{4}$ | B. | $\frac{5}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
7.设双曲线$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{b}$=1的一条渐近线为y=-2x,且一个焦点与抛物线y=$\frac{1}{4}$x2的焦点相同,则此双曲线的方程为( )
| A. | $\frac{5}{4}$x2-5y2=1 | B. | 5y2-$\frac{5}{4}$x2=1 | C. | 5x2-$\frac{5}{4}$y2=1 | D. | $\frac{5}{4}$y2-5x2=1 |
5.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点与抛物线y2=20x的焦点重合,且其渐近线方程为y=±$\frac{4}{3}$x,则双曲线C的方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{64}$=1 | D. | $\frac{{x}^{2}}{64}$-$\frac{{y}^{2}}{36}$=1 |
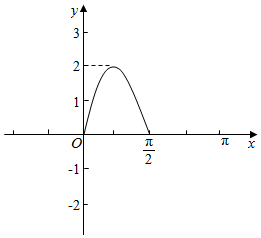 已知函数f(x)=2sinωx(ω>0)的部分图象如图所示.
已知函数f(x)=2sinωx(ω>0)的部分图象如图所示.