题目内容
若两圆(x-a)2+(y-2)2=1与圆x2+y2+2x-48=0相交,则正数a的取值范围是 .
【答案】分析:先写出圆x2+y2+2x-48=0的半径和圆心分别是7,(-1,0),根据两个圆的圆心的距离大于两个圆的半径之差,小于两个圆的半径之和,列出不等式,求出不等式的解.
解答:解:∵两圆(x-a)2+(y-2)2=1与圆x2+y2+2x-48=0相交,
圆x2+y2+2x-48=0的半径和圆心分别是7,(-1,0)
∴两个圆的圆心的距离大于两个圆的半径之差,小于两个圆的半径之和,
即7-1<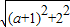 <7+1,
<7+1,
∴6<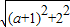 <8,
<8,
∴36<(a+1)2+22<64
∴32<(a+1)2<60
∴正数a的取值范围是
故答案为:
点评:本题考查圆与圆的位置关系,本题解题的关键是根据所给的圆的方程,看出圆心与半径,根据两个圆的位置关系等价的条件写出不等式,本题是一个基础题.
解答:解:∵两圆(x-a)2+(y-2)2=1与圆x2+y2+2x-48=0相交,
圆x2+y2+2x-48=0的半径和圆心分别是7,(-1,0)
∴两个圆的圆心的距离大于两个圆的半径之差,小于两个圆的半径之和,
即7-1<
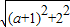 <7+1,
<7+1,∴6<
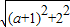 <8,
<8,∴36<(a+1)2+22<64
∴32<(a+1)2<60
∴正数a的取值范围是

故答案为:

点评:本题考查圆与圆的位置关系,本题解题的关键是根据所给的圆的方程,看出圆心与半径,根据两个圆的位置关系等价的条件写出不等式,本题是一个基础题.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目