题目内容
【题目】如图,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为矩形,且平面
为矩形,且平面![]() 与平面
与平面![]() 互相垂直.若多面体
互相垂直.若多面体![]() 的体积为
的体积为![]() ,则该多面体外接球表面积的最小值为( )
,则该多面体外接球表面积的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据题意,设出正方形边长和矩形的高,根据体积公式,求得![]() 等量关系;再找到球心,求得半径,利用导数求函数的最小值,则问题得解.
等量关系;再找到球心,求得半径,利用导数求函数的最小值,则问题得解.
根据题意,连接![]() 交于
交于![]() 点,过
点,过![]() 作
作![]() //
//![]() 交
交![]() 于
于![]() 点,交
点,交![]() 于
于![]() ,连接
,连接![]() .
.
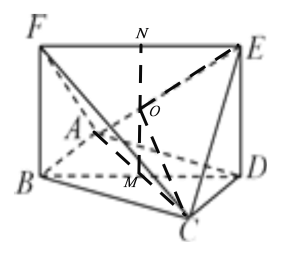
因为四边形![]() 是正方形,故可得
是正方形,故可得![]() ,
,
又因为平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,又
,又![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,
,
不妨设![]() ,
,
故可得多面体![]() 的体积
的体积![]() ;
;
则![]() ,解得
,解得![]() ;
;
又容易知多面体外接球的球心在四边形![]() 外心的垂线上,且为
外心的垂线上,且为![]() 的中点
的中点![]() ,
,
设外接球半径为![]() ,则
,则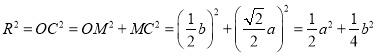 ;
;
将![]() 代入可得
代入可得![]() ,不妨令
,不妨令![]() ,
,
则![]() ,则
,则![]() ,容易知
,容易知![]() 是关于
是关于![]() 的单调增函数,
的单调增函数,
且当![]() 时,
时,![]() ,故可得
,故可得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递减.
单调递减.
故![]() .
.
则外接球表面积的最小值![]() .
.
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目