题目内容
对数列{xn}，满足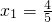
，
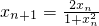；对函数f（x）在（-2，2）上有意义，
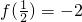，且满足x，y∈（-2，2）时，有
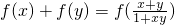成立，则数列{f（xn）}是
- A.以-4为首项以2为公差的等差数列
- B.以-4为首项以2为公比的等比数列
- C.既是等差数列又是等比数列
- D.既不是等差数列又不是等比数列
B
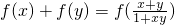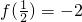分析：本题考查函数特殊值法、等比数列的概念及判定方法．由x，y∈（-2，2）时，有成立，，根据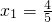，我们可以求出
的值，及
为一常数，则不难判断数列{f（xn）}为一等比数列．
解答：由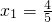，结合已知可得
；
又
，
且
=f（xn）+f（xn）=2f（xn），
于是
，
即{f（xn）}是以-4为首项，以2为公比的等比数列．
故选B
点评：要判断一个数列是否为等差（比）数列，我们常用如下几种办法：①定义法，判断数列连续两项之间的差（比）是否为定值；②等差（比）中项法，判断是否每一项都是其前一项与后一项的等差（比）中项；③通项公式法，判断其通项公式是否为一次（指数）型函数；④前n项和公式法．
分析：本题考查函数特殊值法、等比数列的概念及判定方法．由x，y∈（-2，2）时，有
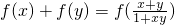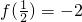成立，，根据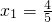，我们可以求出的值，及为一常数，则不难判断数列{f（xn）}为一等比数列．解答：由
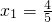，结合已知可得；又
，且
=f（xn）+f（xn）=2f（xn），于是
，即{f（xn）}是以-4为首项，以2为公比的等比数列．
故选B
点评：要判断一个数列是否为等差（比）数列，我们常用如下几种办法：①定义法，判断数列连续两项之间的差（比）是否为定值；②等差（比）中项法，判断是否每一项都是其前一项与后一项的等差（比）中项；③通项公式法，判断其通项公式是否为一次（指数）型函数；④前n项和公式法．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
对数列{xn}，满足x1=
，xn+1=
；对函数f（x）在（-2，2）上有意义，f(-
)=2，且满足x，y，z∈（-2，2）时，有f(x)+f(y)+f(z)=f(
)成立，则f（xn）的表示式为（ ）
| 4 |
| 3 |
| 3xn | ||
1+
|
| 1 |
| 2 |
| x+y+z |
| 1+xyz |
| A、-2n |
| B、3n |
| C、-2×3n |
| D、2×3n |
对数列{xn}，满足x1=
，xn+1=
；对函数f（x）在（-2，2）上有意义，f(
)=-2，且满足x，y∈（-2，2）时，有f(x)+f(y)=f(
)成立，则数列{f（xn）}是（ ）
| 4 |
| 5 |
| 2xn | ||
1+
|
| 1 |
| 2 |
| x+y |
| 1+xy |
| A、以-4为首项以2为公差的等差数列 |
| B、以-4为首项以2为公比的等比数列 |
| C、既是等差数列又是等比数列 |
| D、既不是等差数列又不是等比数列 |
，
；对函数f（x）在上（-1，1）有意义，
，且满足x，y∈（-1，1）时，有
成立，则f（xn）的表示式为（ ）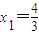
，
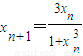；对函数f（x）在（-2，2）上有意义，
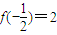，且满足x，y，z∈（-2，2）时，有
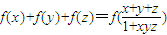成立，则f（xn）的表示式为（ ）