题目内容
对数列{xn}，满足
，
；对函数f（x）在上（-1，1）有意义，
，且满足x，y∈（-1，1）时，有
成立，则f（xn）的表示式为（ ）A．-2n-1
B．2n
C．-2n+1
D．2n+1
【答案】分析：求解析式第一看定义域，此题已经给出（-1，1）；第二看性质：首先奇偶性，代入f（-x）判断其与f（x）的关系，得出奇函数，最后充分分析该题目特征数字，分别求出首项和公比．
解答：解：C由
，结合已知可得
；由x=y=0⇒2f（0）=f（0），
∴f（0）=0，令y=-x，
则f（x）+f（-x）=f（0）=0，
则f（-x）=-f（x）．
又
，
且
=f（xn）+f（xn）=2f（xn），
于是
，即{f（xn）}是以-4为首项，以2为公比的等比数列，
所以f（xn）=-2n+1．
点评：抽象函数本身就给人虚无缥缈的感觉，此题更是配上了形式复杂的数列，但是要坚定题目越是吓人说明找准方向他的命脉就越加薄弱．不仅作对了一道题，而且在这个过程中培养了不畏险阻的意识品质．
解答：解：C由
，结合已知可得；由x=y=0⇒2f（0）=f（0），∴f（0）=0，令y=-x，
则f（x）+f（-x）=f（0）=0，
则f（-x）=-f（x）．
又
，且
=f（xn）+f（xn）=2f（xn），于是
，即{f（xn）}是以-4为首项，以2为公比的等比数列，所以f（xn）=-2n+1．
点评：抽象函数本身就给人虚无缥缈的感觉，此题更是配上了形式复杂的数列，但是要坚定题目越是吓人说明找准方向他的命脉就越加薄弱．不仅作对了一道题，而且在这个过程中培养了不畏险阻的意识品质．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
对数列{xn}，满足x1=
，xn+1=
；对函数f（x）在（-2，2）上有意义，f(-
)=2，且满足x，y，z∈（-2，2）时，有f(x)+f(y)+f(z)=f(
)成立，则f（xn）的表示式为（ ）
| 4 |
| 3 |
| 3xn | ||
1+
|
| 1 |
| 2 |
| x+y+z |
| 1+xyz |
| A、-2n |
| B、3n |
| C、-2×3n |
| D、2×3n |
对数列{xn}，满足x1=
，xn+1=
；对函数f（x）在（-2，2）上有意义，f(
)=-2，且满足x，y∈（-2，2）时，有f(x)+f(y)=f(
)成立，则数列{f（xn）}是（ ）
| 4 |
| 5 |
| 2xn | ||
1+
|
| 1 |
| 2 |
| x+y |
| 1+xy |
| A、以-4为首项以2为公差的等差数列 |
| B、以-4为首项以2为公比的等比数列 |
| C、既是等差数列又是等比数列 |
| D、既不是等差数列又不是等比数列 |
，
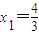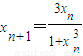；对函数f（x）在（-2，2）上有意义，
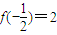，且满足x，y，z∈（-2，2）时，有
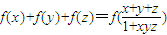成立，则f（xn）的表示式为（ ）