题目内容
对数列{xn}，满足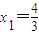
，
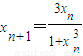；对函数f（x）在（-2，2）上有意义，
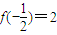，且满足x，y，z∈（-2，2）时，有
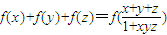成立，则f（xn）的表示式为（ ）A．-2n
B．3n
C．-2×3n
D．2×3n
【答案】分析：由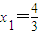
，结合已知可得
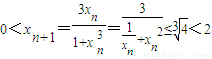．由x=y=z=0可得f（-x）=-f（x）．再根据题设条件能够推出{f（xn）}是以-6为首项，以3为公比的等比数列，由此能够求出f（xn）的表示式．
解答：解：由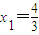
，结合已知可得
；
由x=y=z=0⇒3f（0）=f（0），
∴f（0）=0，令z=0，得f（x）+f（y）=f（x+y），
令y=-x，则f（x）+f（-x）=f（0）=0，
则f（-x）=-f（x）．
又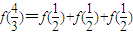
=
，
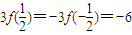且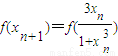
=
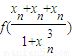=f（xn）+f（xn）+f（xn）=3f（xn），
于是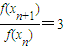
，即{f（xn）}是以-6为首项，以3为公比的等比数列，
所以f（xn）=-2×3n．
点评：本题考查函数奇偶性、特殊值法应用及递推数列通项公式求法．“函数f（x）在上（-2，2）有意义，满足x，y∈（-2，2）时，有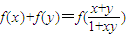
成立，则函数f（x）是奇函数”，这一性质来源于课本习题．本题将其与数列相结合，可谓精工之作．可见，重视课本例、习题很有必要．
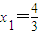，结合已知可得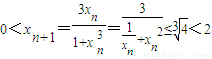．由x=y=z=0可得f（-x）=-f（x）．再根据题设条件能够推出{f（xn）}是以-6为首项，以3为公比的等比数列，由此能够求出f（xn）的表示式．解答：解：由
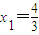，结合已知可得；由x=y=z=0⇒3f（0）=f（0），
∴f（0）=0，令z=0，得f（x）+f（y）=f（x+y），
令y=-x，则f（x）+f（-x）=f（0）=0，
则f（-x）=-f（x）．
又
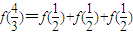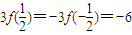=，且
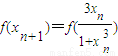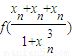==f（xn）+f（xn）+f（xn）=3f（xn），于是
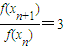，即{f（xn）}是以-6为首项，以3为公比的等比数列，所以f（xn）=-2×3n．
点评：本题考查函数奇偶性、特殊值法应用及递推数列通项公式求法．“函数f（x）在上（-2，2）有意义，满足x，y∈（-2，2）时，有
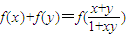成立，则函数f（x）是奇函数”，这一性质来源于课本习题．本题将其与数列相结合，可谓精工之作．可见，重视课本例、习题很有必要． 
练习册系列答案
小学课时特训系列答案
相关题目
对数列{xn}，满足x1=
，xn+1=
；对函数f（x）在（-2，2）上有意义，f(-
)=2，且满足x，y，z∈（-2，2）时，有f(x)+f(y)+f(z)=f(
)成立，则f（xn）的表示式为（ ）
| 4 |
| 3 |
| 3xn | ||
1+
|
| 1 |
| 2 |
| x+y+z |
| 1+xyz |
| A、-2n |
| B、3n |
| C、-2×3n |
| D、2×3n |
对数列{xn}，满足x1=
，xn+1=
；对函数f（x）在（-2，2）上有意义，f(
)=-2，且满足x，y∈（-2，2）时，有f(x)+f(y)=f(
)成立，则数列{f（xn）}是（ ）
| 4 |
| 5 |
| 2xn | ||
1+
|
| 1 |
| 2 |
| x+y |
| 1+xy |
| A、以-4为首项以2为公差的等差数列 |
| B、以-4为首项以2为公比的等比数列 |
| C、既是等差数列又是等比数列 |
| D、既不是等差数列又不是等比数列 |
，
；对函数f（x）在上（-1，1）有意义，
，且满足x，y∈（-1，1）时，有
成立，则f（xn）的表示式为（ ）