题目内容
设△ABC的内角A,B,C的对边分别为a,b,c,已知向量, ,
, ,
, ,
, ,
, .
.
(1)求cosA的值;
(2)求△ABC的面积S.
解:(1) ,
, ,
, ,
, ,
, .
.
∴a•cosA-c•cosB=a•cos(B+C)+b•cosC,即 2a•cosA=c•cosB++b•cosC.
再由正弦定理可得 2sinAcosA=sinCcosB cosCsinB=sin(B+C)=sinA,由于sinA≠0,∴cosA= .
.
(2)由(1)可得cosA= ,A=
,A= .
.
△ABC中,由余弦定理可得 13=b2+16-8bcosA=b2+16-4b,解得 b=5或 b=-1 (舍去).
故△ABC的面积S=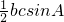 =5
=5 .
.
分析:(1)由 化简可得2a•cosA=c•cosB++b•cosC,再由正弦定理可得 2sinAcosA=sinA,求出cosA=
化简可得2a•cosA=c•cosB++b•cosC,再由正弦定理可得 2sinAcosA=sinA,求出cosA= .
.
(2)由(1)可得cosA= ,A=
,A= .△ABC中,由余弦定理求出b的值,再根据△ABC的面积S=
.△ABC中,由余弦定理求出b的值,再根据△ABC的面积S=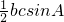 ,运算求得结果.
,运算求得结果.
点评:本题主要考查两个向量的数量积公式,以及正弦定理、余弦定理的应用,属于中档题.
 ,
, ,
, ,
, ,
, .
.∴a•cosA-c•cosB=a•cos(B+C)+b•cosC,即 2a•cosA=c•cosB++b•cosC.
再由正弦定理可得 2sinAcosA=sinCcosB cosCsinB=sin(B+C)=sinA,由于sinA≠0,∴cosA=
 .
.(2)由(1)可得cosA=
 ,A=
,A= .
.△ABC中,由余弦定理可得 13=b2+16-8bcosA=b2+16-4b,解得 b=5或 b=-1 (舍去).
故△ABC的面积S=
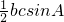 =5
=5 .
.分析:(1)由
 化简可得2a•cosA=c•cosB++b•cosC,再由正弦定理可得 2sinAcosA=sinA,求出cosA=
化简可得2a•cosA=c•cosB++b•cosC,再由正弦定理可得 2sinAcosA=sinA,求出cosA= .
.(2)由(1)可得cosA=
 ,A=
,A= .△ABC中,由余弦定理求出b的值,再根据△ABC的面积S=
.△ABC中,由余弦定理求出b的值,再根据△ABC的面积S=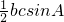 ,运算求得结果.
,运算求得结果.点评:本题主要考查两个向量的数量积公式,以及正弦定理、余弦定理的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目