题目内容
已知坐标平面上点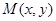 与两个定点
与两个定点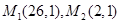 的距离之比等于5.
的距离之比等于5.
(1)求点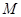 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为 ,过点
,过点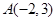 的直线
的直线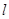 被
被 所截得的线段的长为8,求直线
所截得的线段的长为8,求直线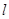 的方程
的方程
(1)点M的轨迹方程是(x-1)2+(y-1)2=25,轨迹是以(1,1)为圆心,以5为半径的圆
(2)直线l的方程为x=-2,或5x-12y+46=0.
解析试题分析:解:(1)由题意,得 =5.
=5.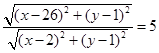 ,化简,得x2+y2-2x-2y-23=0.即(x-1)2+(y-1)2=25.∴点M的轨迹方程是(x-1)2+(y-1)2=25,轨迹是以(1,1)为圆心,以5为半径的圆.
,化简,得x2+y2-2x-2y-23=0.即(x-1)2+(y-1)2=25.∴点M的轨迹方程是(x-1)2+(y-1)2=25,轨迹是以(1,1)为圆心,以5为半径的圆.
(2)当直线l的斜率不存在时,l:x=-2,此时所截得的线段的长为 ,∴l:x=-2符合题意.当直线l的斜率存在时,设l的方程为y-3=k(x+2),即kx-y+2k+3=0,圆心到l的距离
,∴l:x=-2符合题意.当直线l的斜率存在时,设l的方程为y-3=k(x+2),即kx-y+2k+3=0,圆心到l的距离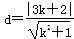 ,由题意,得
,由题意,得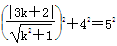 ,解得
,解得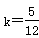 .∴直线l的方程为
.∴直线l的方程为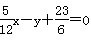 .即5x-12y+46=0.综上,直线l的方程为x=-2,或5x-12y+46=0.
.即5x-12y+46=0.综上,直线l的方程为x=-2,或5x-12y+46=0.
考点:圆的方程
点评:解决的关键是根据直接法来得到点满足的几何关系,然后坐标化得到求解,并能结合直线与圆的位置关系来得到,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
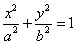 (a>b>0)的离心率为
(a>b>0)的离心率为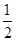 ,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+
,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+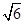 相切.
相切.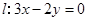 与椭圆在
与椭圆在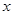 轴上方的一个交点为
轴上方的一个交点为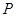 ,
,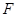 是椭圆的右焦点,试探究以
是椭圆的右焦点,试探究以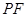 为
为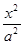 +
+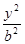 =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F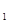 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF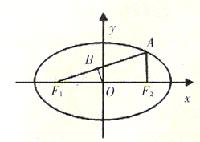
 +y
+y ,y
,y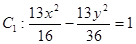 ,点
,点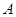 、
、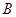 分别为双曲线
分别为双曲线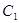 的左、右焦点,动点
的左、右焦点,动点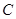 在
在 轴上方.
轴上方.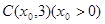 是双曲线的一条渐近线上的点,求以
是双曲线的一条渐近线上的点,求以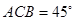 ,求△
,求△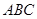 的外接圆的方程;
的外接圆的方程;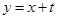 上任取一点
上任取一点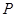 ,从点
,从点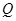 . 问是否存在一个定点
. 问是否存在一个定点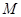 ,恒有
,恒有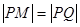 ?请说明理由.
?请说明理由.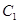 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为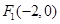 ,
,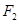
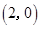 ,点
,点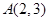 在椭圆
在椭圆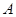 的直线
的直线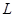 与抛物线
与抛物线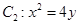 交于
交于 两点,抛物线
两点,抛物线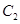 在点
在点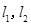 ,且
,且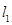 与
与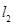 交于点
交于点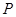 .
.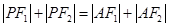 的点
的点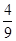 ,求顶点A的轨迹方程.?
,求顶点A的轨迹方程.?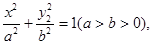 左、右焦点分别为F1、F2,焦距为4,点M是椭圆C上一点,满足
左、右焦点分别为F1、F2,焦距为4,点M是椭圆C上一点,满足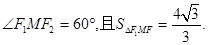
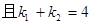 ,求证:直线AB过定点,并求出直线AB的斜率k的取值范围。
,求证:直线AB过定点,并求出直线AB的斜率k的取值范围。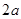 ,焦点是
,焦点是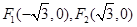 ,点
,点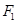 到直线
到直线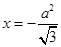 的距离为
的距离为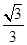 ,过点
,过点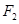 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于
与椭圆交于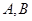 两点,使得
两点,使得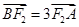 .
.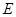 上任意一点
上任意一点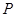 到两个定点
到两个定点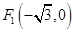 ,
,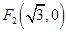 的距离之和为4.
的距离之和为4.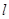 与曲线
与曲线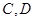 两点,且
两点,且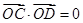 (
(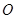 为原点),求直线
为原点),求直线