题目内容
已知椭圆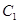 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为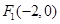 ,
,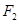
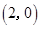 ,点
,点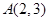 在椭圆
在椭圆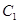 上,过点
上,过点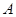 的直线
的直线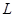 与抛物线
与抛物线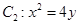 交于
交于 两点,抛物线
两点,抛物线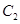 在点
在点 处的切线分别为
处的切线分别为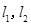 ,且
,且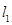 与
与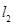 交于点
交于点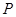 .
.
(1) 求椭圆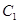 的方程;
的方程;
(2) 是否存在满足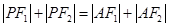 的点
的点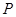 ? 若存在,指出这样的点
? 若存在,指出这样的点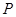 有几个(不必求出点
有几个(不必求出点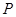 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
(1) . (2)满足条件的点
. (2)满足条件的点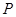 有两个.
有两个.
解析(1)试题分析:解法1:设椭圆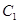 的方程为
的方程为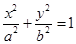
 ,依题意:
,依题意: 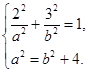
解得: 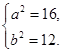 ∴ 椭圆
∴ 椭圆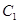 的方程为
的方程为 .
.
解法2:设椭圆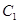 的方程为
的方程为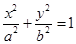
 ,根据椭圆的定义得
,根据椭圆的定义得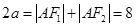 ,即
,即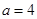 , ∵
, ∵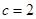 , ∴
, ∴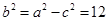 . ∴ 椭圆
. ∴ 椭圆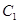 的方程为
的方程为 .
.
(2) 解法1:显然直线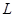 的斜率存在,设直线
的斜率存在,设直线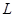 的方程为
的方程为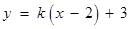 ,
,
由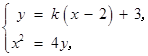 消去
消去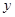 ,得
,得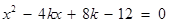 .
.
设 ,则
,则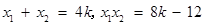 .
.
由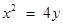 ,即
,即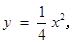 得
得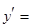
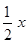 .
.
∴抛物线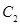 在点
在点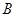 处的切线
处的切线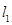 的方程为
的方程为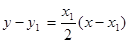 ,即
,即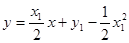 .
.
∵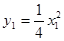 , ∴
, ∴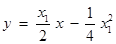 .
.
同理,得抛物线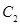 在点
在点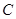 处的切线
处的切线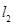 的方程为
的方程为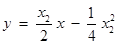 .
.
由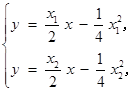 解得
解得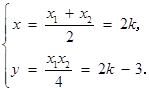
∴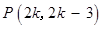 . ∵
. ∵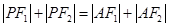 ,
,
∴点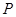 在椭圆
在椭圆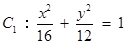 上. ∴
上. ∴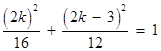 .
.
化简得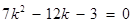 .(*) 由
.(*) 由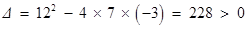 ,
,
可得方程(*)有两个不等的实数根. ∴满足条件的点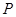 有两个.
有两个.
解法2:设点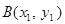 ,
,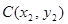 ,
,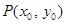 ,由
,由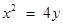 ,即
,即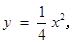 得
得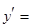
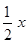 .
.
∴抛物线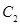 在点
在点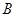 处的切线
处的切线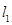 的方程为
的方程为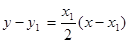 ,
,
即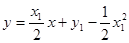 .∵
.∵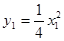 , ∴
, ∴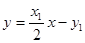 .
.
∵点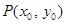 在切线
在切线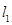 上, ∴
上, ∴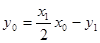 . ①
. ①
同理, 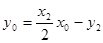 . ② 综合①、②得,点
. ② 综合①、②得,点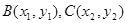 的坐标都满足方程
的坐标都满足方程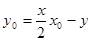 .∵经过
.∵经过
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
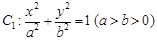 的离心率为
的离心率为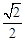 ,
, 轴被曲线
轴被曲线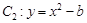 截得的线段长等于
截得的线段长等于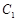 的短轴长。
的短轴长。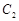 与
与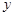 轴的交点为
轴的交点为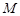 ,过坐标原点
,过坐标原点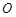 的直线
的直线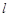 与
与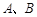 ,直线
,直线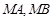 分别与
分别与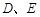 。
。
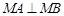 。
。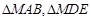 的面积分别为
的面积分别为 ,若
,若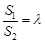 ,求
,求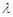 的取值范围。
的取值范围。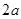 ,焦点是
,焦点是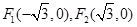 ,点
,点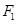 到直线
到直线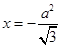 的距离为
的距离为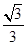 ,过点
,过点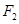 且倾斜角为锐角的直线
且倾斜角为锐角的直线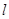 与椭圆交于A、B两点,使得|
与椭圆交于A、B两点,使得|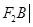 =3|
=3|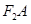
 .
.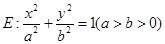 的右焦点
的右焦点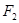 与抛物线
与抛物线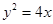 的焦点重合,过
的焦点重合,过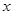 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于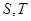 ,而与抛物线交于
,而与抛物线交于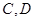 两点,且
两点,且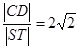 .
.
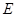 的方程;
的方程; 的直线与椭圆
的直线与椭圆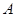 和
和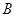 ,
, 为椭圆
为椭圆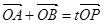 (
(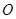 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围. (α为参数).
(α为参数).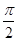 ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;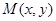 与两个定点
与两个定点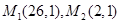 的距离之比等于5.
的距离之比等于5.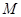 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形; ,过点
,过点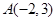 的直线
的直线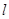 被
被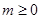 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量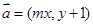 ,向量
,向量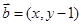 ,
, ,动点
,动点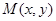 的轨迹为E.
的轨迹为E.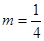 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且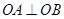 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程; 与圆C:
与圆C: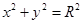 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且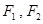 为椭圆
为椭圆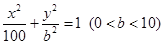 的左、右焦点,
的左、右焦点,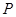 是椭圆上一点,若
是椭圆上一点,若 。
。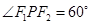 求
求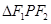 的面积。
的面积。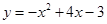 与它在点
与它在点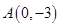 和点
和点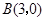 的切线所围成的区域的面积。
的切线所围成的区域的面积。