Question

【题目】在中，，，有下述四个结论：

①若为的重心，则

②若为边上的一个动点，则为定值2

③若，为边上的两个动点，且，则的最小值为

④已知为内一点，若，且，则的最大值为2

其中所有正确结论的编号是（ ）

A.①③B.①④C.②③D.②④

Answer 1

【答案】A

【解析】

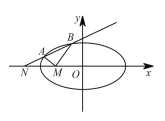
根据题意，先得为等腰直角三角形；①取中点为，连接，得到，根据平面向量基本定理，即可得出结果；②先由①得到，由题意得到在上的投影为，进而可求出向量数量积；③以点为坐标原点，分别以、所在直线为轴、轴，建立平面直角坐标系，由题意，设，且，不妨令，根据向量数量积的坐标表示，即可求出结果；④同③建立平面直角坐标系，设，根据题意，得到，再设，由题意，得到，，用表示出，即可求出结果；

因为在中，，； 所以为等腰直角三角形；

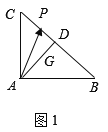
①如图1，取中点为，连接，因为为的重心，

所以在上，且，

所以，故①正确；

②如图1，同①，因为为中点，为等腰直角三角形，所以，

若为边上的一个动点，则在上的投影为，

因此，故②错；

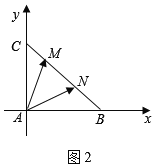
③如图2，以点为坐标原点，分别以、所在直线为轴、轴，建立如图所示的平面直角坐标系，则，，，易得，所在直线方程为：；

因为，为边上的两个动点，

所以设，，且，不妨令，

因为，所以，即，则，

所以

，当且仅当时，等号成立；故③正确；

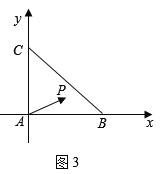
④同③建立如图3所示的平面直角坐标系，则，，

设，则，

又，所以，即

因为为内一点，且，设，

则，且，，

因此，

因为，所以，所以无最值，即无最值，故④错.

故选：A.