题目内容
)已知四边形ABCD满足AD∥BC,BA=AD=DC=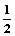 BC=a,E是BC的中点,将△BAE沿AE折起到
BC=a,E是BC的中点,将△BAE沿AE折起到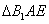 的位置,使平面
的位置,使平面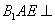 平面
平面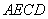 ,F为B1D的中点.
,F为B1D的中点.
(Ⅰ)证明:B1E∥平面ACF;
(Ⅱ)求平面ADB1与平面ECB1所成锐二面角的余弦值.
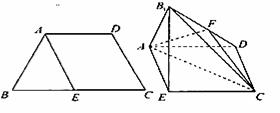
(1)连结ED交AC于O,连结OF,因为AECD为菱形,OE=OD所以FO∥B1E, 所以 。………………4分
。………………4分
(2) 取AE的中点M,连结B1M,连结MD,则∠AMD= ,
,
分别以ME,MD,MB1为x,y,z轴建系,则 ,
,
 ,
, ,
, ,所以1,
,所以1, ,
, ,
, ,设面ECB1的法向量为
,设面ECB1的法向量为 ,
, ,令x=1,
,令x=1,  ,…8分
,…8分
同理面ADB1的法向量为 …………10分
…………10分
所以 ,
,
故面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 ………… 12分
………… 12分

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 上且
上且 =
=
 ,N为B1B的中点,则|
,N为B1B的中点,则| |为( )
|为( ) B.
B. C.
C.  D.
D. 
 、
、 、
、 、
、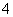 、
、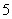 、
、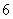 个点)两次,落在水平桌面后,记正面朝上的点数分别为
个点)两次,落在水平桌面后,记正面朝上的点数分别为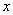 ,
,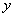 ,设事件
,设事件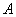 为“
为“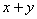 为偶数”, 事件
为偶数”, 事件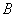 为
为 ”,则概率
”,则概率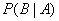 等于 。
等于 。 ②2ab ③a2+b2 ④a
②2ab ③a2+b2 ④a -
-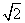 ≥a+
≥a+ -2.
-2.