题目内容
4.复数z•(1+i)=|1+$\sqrt{3}i}$|,则z=( )| A. | 2-2i | B. | 1-i | C. | 2+2i | D. | 1+i |
分析 根据复数的概念与代数运算法则,进行计算即可.
解答 解:∵z(1+i)=2,
z=$\frac{2}{1+i}$=$\frac{2(1-i)}{(1+i)(1-i)}$=1-i.
故选:B.
点评 本题考查了复数的概念与代数运算法则的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知f(x)=sin(x+1)$\frac{π}{3}$-$\sqrt{3}$cos(x+1)$\frac{π}{3}$,则f(1)+f(2)+f(3)+…+f(2011)=( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 0 |
12.已知全集U=R,集合M={x|log${\;}_{\frac{1}{2}}$(x-1)>-1},N={x|1<2x<4},则(∁UM)∩N=( )
| A. | {0|0<x≤3} | B. | {x|1<x≤3} | C. | {x|0<x≤1} | D. | {x|1<x<2} |
19.$\frac{3π}{5}$弧度化为角度是( )
| A. | 110° | B. | 160° | C. | 108° | D. | 218° |
16.设f(x)是R上的偶函数,并且在[0,+∞)上单调递减,则f(-1),f(-3),f(5)的大小顺序是( )
| A. | f(-1)>f(-3)>f(5) | B. | f(-1)>f(5)>f(-3) | C. | f(5)>f(-1)>f(-3) | D. | f(-3)>f(-1)>f(5) |
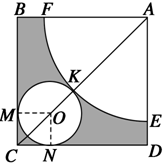 如图所示,在边长为$5+\sqrt{2}$的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.
如图所示,在边长为$5+\sqrt{2}$的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.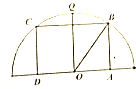 如图,四边形ABCD是半径为1的半圆O的内接矩形,其中A、D在直径上,Q为弧CB的中点,设∠BOQ=θ,记f(θ)=$\frac{1}{OA}$+$\frac{1}{AB}$,求f(θ)的最小值.
如图,四边形ABCD是半径为1的半圆O的内接矩形,其中A、D在直径上,Q为弧CB的中点,设∠BOQ=θ,记f(θ)=$\frac{1}{OA}$+$\frac{1}{AB}$,求f(θ)的最小值.