题目内容
等腰梯形的周长为60，底角为60°，问这梯形各边长为多少时，面积最大？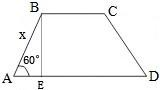
分析：设等腰梯形的腰长为x，利用x表达出梯形的面积，转化为求函数的最值问题．
解答：解：设等腰梯形的腰长为x，（0＜x＜30），则有
AE=
，BE=
，BC=
=
=
．
等腰梯形ABCD的面积=
•BE
=（BC+AE）•BE
=(
+
)•
x
=
(30x-x2)
=
[225-(x-15)2]．
由此可知，当且仅当x=15时等腰梯形的面积最大．此时，腰AB=CD=x=15，上底BC=7.5，
下底AD=BC+2AE=22.5．
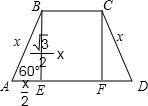
AE=
| x |
| 2 |
| ||
| 2 |
| 60-2•AB-2AE |
| 2 |
| 60-2x-x |
| 2 |
| 60-3x |
| 2 |
等腰梯形ABCD的面积=
| BC+AD |
| 2 |
=（BC+AE）•BE
=(
| 60-3x |
| 2 |
| x |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
=
| ||
| 2 |
由此可知，当且仅当x=15时等腰梯形的面积最大．此时，腰AB=CD=x=15，上底BC=7.5，
下底AD=BC+2AE=22.5．
点评：本题考查函数的应用，求函数关系式和最值，难度不大，要充分结合图形表达各边长．
练习册系列答案
相关题目
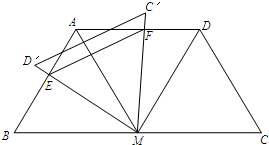（2012•大丰市一模）已知：如图，M是线段BC的中点，BC=4，分别以MB、MC为边在线段BC的同侧作等边△BAM、等边△MCD，连接AD．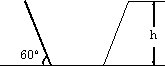
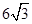m2，为了使堤的上面与两侧面的水泥用料最省，要求断面的外周长（梯形的上底BC与两腰长的和）最小．如何设计防洪堤，才能使水泥用料最省．
