题目内容
15．若cos（75°+α）=$\frac{1}{3}$，则cos（30°-2α）的值为（ ）| A． | $\frac{4\sqrt{2}}{9}$ | B． | -$\frac{4\sqrt{2}}{9}$ | C． | $\frac{7}{9}$ | D． | -$\frac{7}{9}$ |
分析 利用同角三角函数基本关系式以及二倍角公式化简求解即可．
解答 解：cos（75°+α）=$\frac{1}{3}$，可得sin（15°-α）=$\frac{1}{3}$．
cos（30°-2α）=1-2sin2（15°-α）=1-2×$\frac{1}{9}$=$\frac{7}{9}$．
故选：C．
点评 本题考查二倍角公式以及诱导公式的应用，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
5．直线l：x-2y+2=0过椭圆$\frac{x^2}{5}+\frac{y^2}{b^2}=1$$（0＜b＜\sqrt{5}）$的一个顶点．则该椭圆的离心率为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{{\sqrt{5}}}{5}$ | D． | $\frac{{2\sqrt{5}}}{5}$ |
6．设命题P：?n∈N，f（n）≤n，则￢p是（ ）
| A． | ?n∉N，f（n）＞n | B． | ?n0∈N，f（n0）＞n0 | C． | ?n0∈N，f（n0）≤n0 | D． | ?n∈N，f（n）＞n |
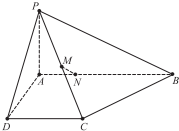如图，在四棱锥P-ABCD中，已知AB⊥AD，AD⊥DC．PA⊥底面ABCD，且AB=2，PA=AD=DC=1，M为PC的中点，N在AB上，且BN=3AN．
7．复数z=$\frac{m-2i}{1-2i}$（m∈R）不可能在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
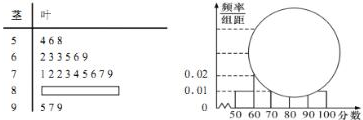某校高一某班的一次数学测试成绩（满分为100分）的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图，据此解答如下问题；