题目内容
(本题满分12分)在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(Ⅰ)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ)随机变量 的最大值为5,概率
的最大值为5,概率 ;
;
(Ⅱ)
| 0 | 1 | 2 | 5 |
P |
|
|
|
|
期望为2
【解析】
试题分析:(Ⅰ)∵x、y可能的取值为1、2、3, 1分
∴ ,
,
∴ ,且当x=1,y=3或x=3,y=1时,
,且当x=1,y=3或x=3,y=1时, =5.
=5.
因此,随机变量 的最大值为5 3分
的最大值为5 3分
有放回摸两球的所有情况有3×3=9种∴ 6分
6分
(Ⅱ) 的所有取值为0,1,2,5.
的所有取值为0,1,2,5.
∵ =0时,x=2,y=2这一种情况.
=0时,x=2,y=2这一种情况.
 =1时,有x=1,y=1或x=2,y=1或x=2,y=3或x=3,y=3四种情况,
=1时,有x=1,y=1或x=2,y=1或x=2,y=3或x=3,y=3四种情况,
 =2时,有x=1,y=2或x=3,y=2两种情况.
=2时,有x=1,y=2或x=3,y=2两种情况.
∴ 8分
8分
则随机变量 的分布列为: 10分
的分布列为: 10分
| 0 | 1 | 2 | 5 |
P |
|
|
|
|
因此,数学期望为
 12分
12分
考点:本题考查离散型随机变量期望与方差,古典概型的概率

练习册系列答案
相关题目



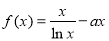 .
. 在
在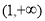 上为减函数,求实数
上为减函数,求实数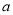 的最小值;
的最小值;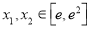 ,使
,使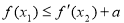 成立,求实数
成立,求实数 与直线
与直线 互相垂直,那么
互相垂直,那么 的值等于 ( )
的值等于 ( ) C.
C. D.
D.
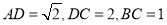 ,它可能随机在草原上任何一处(点),若落在扇形沼泽区域ADE以外丹顶鹤能生还,则该丹顶鹤生还的概率是( )
,它可能随机在草原上任何一处(点),若落在扇形沼泽区域ADE以外丹顶鹤能生还,则该丹顶鹤生还的概率是( )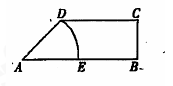
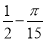 B.
B.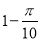 C.
C.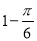 D.
D.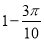
 ,则图中阴影部分表示的集合为
,则图中阴影部分表示的集合为
 B.
B. C.
C. D.
D.
 ,则
,则 = .
= . 是
是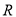 上的奇函数,且在区间
上的奇函数,且在区间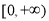 上单调递增,若
上单调递增,若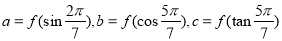 ,则 ( )
,则 ( )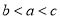 B.
B.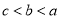 C.
C.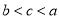 D.
D.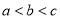
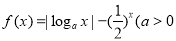 且
且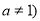 有两个零点
有两个零点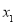 、
、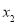 ,则有( )
,则有( )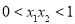 (B)
(B)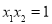 (C)
(C)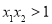 (D)
(D)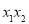 的范围不确定
的范围不确定 =
= ,若对
,若对
 ,
, ∈(0,1),且
∈(0,1),且 ,都有
,都有 为真命题,则实数
为真命题,则实数 的取值范围 .
的取值范围 .