题目内容
如图，△ABC的外角平分线AD交外接圆于D，若DB=
，则DC= ．
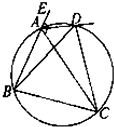
| 3 |
考点：相似三角形的性质
专题：选作题,解三角形
分析：利用四点共圆的性质和同圆弧所对的圆周角相等的性质、角平分线的性质即可得出．
解答：解：∵A、B、C、D共圆，∴∠DAE=∠BCD．
又∵∠DAC=∠DBC，∠DAE=∠DAC，
∴∠DBC=∠DCB，
∴CD=BD=
．
故答案为：
．
又∵∠DAC=∠DBC，∠DAE=∠DAC，
∴∠DBC=∠DCB，
∴CD=BD=
| 3 |
故答案为：
| 3 |
点评：熟练掌握四点共圆的性质和同圆弧所对的圆周角相等的性质、角平分线的性质是解题的关键．
练习册系列答案
相关题目
已知实数m，n，若m≥0，n≥0，且m+n=1，则
+
的最小值为（ ）
| m2 |
| m+2 |
| n2 |
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
处理框正确的画法是（ ）
A、 | B、 | C、 | D、 |
在（xy-x-2y+2）6的展开式中，xy2的系数是（ ）
| A、2880 | B、1440 | C、-2880 | D、-1440 |
使得（3x2+
）n（n∈N+）的展开式中含有常数项的最小的n=（ ）
| 2 |
| x3 |
| A、3 | B、5 | C、6 | D、10 |
如图，AB为⊙O的弦，C是弧AB的中点，过点B作直线BD，连接CD交AB于点N，若∠CDB=30°，则∠CNB=一个二面角的两个面分别垂直于另一个二面角的两个面，那么这两个二面角（ ）
| A、相等 | B、互补 | C、相等或互补 | D、不能确定 |