题目内容
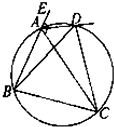
 如图,AB为⊙O的弦,C是弧AB的中点,过点B作直线BD,连接CD交AB于点N,若∠CDB=30°,则∠CNB=
如图,AB为⊙O的弦,C是弧AB的中点,过点B作直线BD,连接CD交AB于点N,若∠CDB=30°,则∠CNB=考点:圆內接多边形的性质与判定
专题:选作题,几何证明
分析:连接OC,则OC⊥AB,∠OCD=∠ODC,即可得出结论.
解答: 解:连接OC,则OC⊥AB,∠OCD=∠ODC,
解:连接OC,则OC⊥AB,∠OCD=∠ODC,
∵∠CDB=30°,
∴∠CNB=90°-30°=60°.
故答案为:60°.
 解:连接OC,则OC⊥AB,∠OCD=∠ODC,
解:连接OC,则OC⊥AB,∠OCD=∠ODC,∵∠CDB=30°,
∴∠CNB=90°-30°=60°.
故答案为:60°.
点评:本题考查垂径定理,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从0,1,2,3,4这五个数字中任取一个奇数和两个偶数,可以组成没有重复数字的三位数的个数为( )
| A、12 | B、16 | C、20 | D、28 |
圆内接四边形ABCD中,cosA+cosB+cosC+cosD等于( )
| A、0 | B、4 | C、2 | D、不确定 |
在平面直角坐标系中,曲线C:x2-y2=36经过伸缩变换
后,所得曲线的焦点坐标为( )
|
A、(0,±
| ||
B、(±
| ||
C、(0,±
| ||
D、(±
|
 ,
,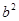 },则
},则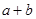 = .
= .