题目内容
已知f(x)=2+log3x,x∈［1,9］,求y=［f(x)］2+f(x2)的最大值及y取最大值时x的值.
思路分析:要求函数y=［f(x)］2+f(x2)的最大值,要做两件事,一是要求其表达式;二是要求出它的定义域,然后求值域.
解:∵f(x)=2+log3x,
∴y=［f(x)］2+f(x2)=(2+log3x)2+2+log
=(2+log3x)2+2+2log3x
=log32x+6log3x+6
=(log3x+3)2-3.
∵函数f(x)的定义域为［1,9］,
∴要使函数y=［f(x)］2+f(x2)有定义,就需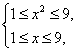
∴1≤x≤3.∴0≤log3x≤1.
∴6≤y=(log3x+3)2-3≤13.
∴当x=3时,函数y=［f(x)］2+f(x2)取最大值13.
说明:本例正确求解的关键是:函数y=［f(x)］2+f(x2)定义域的正确确定.如果我们误认为［1,9］是它的定义域,则将求得错误的最大值22.
其实我们还能求出函数y=［f(x)］2+f(x2)的值域为［6,13］.
练习册系列答案
快乐5加2金卷系列答案
相关题目
（2012•潍坊二模）如图，已知F（2，0）为椭圆
R)，
=
2x2+3x-1，h (x)为f
(x)、g(x)在R上生成的一个二次函数.
，若h (x)为偶函数，求
；
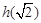，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；