题目内容
(一、二级达标校做)
已知函数f(x)=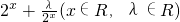 .
.
(Ⅰ) 讨论函数的f(x)奇偶性,并说明理由;
(Ⅱ)当λ=1时,讨论方程f(x)=μ(μ∈R)在x∈[-1,1]上实数解的个数情况,并说明理由.
解:(Ⅰ)∵x∈R,定义域关于原点对称.
当λ=1时,f(-x)= =
= =f(x),此时f(x)为偶函数.
=f(x),此时f(x)为偶函数.
当λ=-1时,f(-x)= =
= =-f(x),此时f(x)为奇函数.
=-f(x),此时f(x)为奇函数.
当λ≠±1时,f(-x)= ,显然f(-x)≠f(x),且 f(-x)≠-f(x),故f(x)为非奇非偶函数.
,显然f(-x)≠f(x),且 f(-x)≠-f(x),故f(x)为非奇非偶函数.
(Ⅱ)当λ=1时,f(x)= ,方程f(x)=μ(μ∈R),即
,方程f(x)=μ(μ∈R),即  =μ.
=μ.
令t=2x,由于-1≤x≤1,∴ ≤t≤2.
≤t≤2.
再由 g(t)=t+ 在[
在[ ,1]上是减函数,在[1,2]上是增函数.
,1]上是减函数,在[1,2]上是增函数.
∴g(t)的最小值为g(1)=2,最大值为f( )=
)= ,或 g(2)=
,或 g(2)= ,
,
故 g(t)的值域为[2,2],方程即t+ =μ.
=μ.
当μ<2或μ> 时,解的个数为0;
时,解的个数为0;
当μ=2时,解的个数为1;
当2<μ≤ 解的个数为2.
解的个数为2.
分析:(Ⅰ)定义域R关于原点对称,分λ=1、λ=-1、λ≠±1三种情况分别利用奇函数和偶函数的定义判断函数的奇偶性.
(Ⅱ)方程即 =μ,令t=2x,由于-1≤x≤1,可得
=μ,令t=2x,由于-1≤x≤1,可得  ≤t≤2,g(t)=t+
≤t≤2,g(t)=t+ 的值域为[2,2],由此求出方程t+
的值域为[2,2],由此求出方程t+ =μ的实数解的个数.
=μ的实数解的个数.
点评:本题主要考查方程的根的存在性及个数判断,函数的奇偶性的判断,体现了转化和分类讨论的数学思想,属于中档题.
当λ=1时,f(-x)=
 =
= =f(x),此时f(x)为偶函数.
=f(x),此时f(x)为偶函数.当λ=-1时,f(-x)=
 =
= =-f(x),此时f(x)为奇函数.
=-f(x),此时f(x)为奇函数.当λ≠±1时,f(-x)=
 ,显然f(-x)≠f(x),且 f(-x)≠-f(x),故f(x)为非奇非偶函数.
,显然f(-x)≠f(x),且 f(-x)≠-f(x),故f(x)为非奇非偶函数.(Ⅱ)当λ=1时,f(x)=
 ,方程f(x)=μ(μ∈R),即
,方程f(x)=μ(μ∈R),即  =μ.
=μ.令t=2x,由于-1≤x≤1,∴
 ≤t≤2.
≤t≤2.再由 g(t)=t+
 在[
在[ ,1]上是减函数,在[1,2]上是增函数.
,1]上是减函数,在[1,2]上是增函数.∴g(t)的最小值为g(1)=2,最大值为f(
 )=
)= ,或 g(2)=
,或 g(2)= ,
,故 g(t)的值域为[2,2],方程即t+
 =μ.
=μ.当μ<2或μ>
 时,解的个数为0;
时,解的个数为0;当μ=2时,解的个数为1;
当2<μ≤
 解的个数为2.
解的个数为2.分析:(Ⅰ)定义域R关于原点对称,分λ=1、λ=-1、λ≠±1三种情况分别利用奇函数和偶函数的定义判断函数的奇偶性.
(Ⅱ)方程即
 =μ,令t=2x,由于-1≤x≤1,可得
=μ,令t=2x,由于-1≤x≤1,可得  ≤t≤2,g(t)=t+
≤t≤2,g(t)=t+ 的值域为[2,2],由此求出方程t+
的值域为[2,2],由此求出方程t+ =μ的实数解的个数.
=μ的实数解的个数.点评:本题主要考查方程的根的存在性及个数判断,函数的奇偶性的判断,体现了转化和分类讨论的数学思想,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 (一、二级达标校做)
(一、二级达标校做)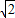 .
.
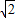 .
.