题目内容
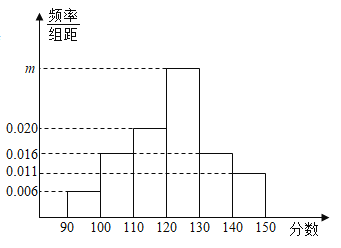
【题目】（多选）统计某校
名学生的某次数学同步练习成绩（满分150分），根据成绩依次分成六组：
，
，
，
，
，
，得到频率分布直方图如图所示，若不低于140分的人数为110，则下列说法正确的是（ ）
A.
B.
C.100分以下的人数为60D.成绩在区间
内的人数占大半
【答案】AC
【解析】
对A，通过频率分布直方图中各小长方形的面积和为1，计算得出
的值；对B，通过不低于140分的人数和频率，计算出总人数
的值；对C，通过计算出的总人数和100分以下的的频率，计算出100分以下的人数；对D，计算成绩在区间
的频率和，看频率和是否大于0.5.
对选项A，由图可知，
，解得
，故A说法正确；
对选项B，因为不低于140分的频率为
，所以
，故B说法错误；
对选项C，因为100分以下的频率为
，所以100分以下的人数为
，故C说法正确；
对选项D，成绩在区间内的频率为
，人数占小半，故D说法错误.
故选：AC
【题目】某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面列联表：
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
（1）分别估计男、女顾客对该商场服务满意的概率；
（2）能否有
的把握认为男、女顾客对该商场服务的评价有差异？
【题目】交通部门调查在高速公路上的平均车速情况，随机抽查了60名家庭轿车驾驶员，统计其中有40名男性驾驶员，其中平均车速超过
的有30人，不超过的有10人；在其余20名女性驾驶员中，平均车速超过的有5人，不超过的有15人.
（1）完成下面的
列联表，并据此判断是否有
的把握认为，家庭轿车平均车速超过与驾驶员的性别有关；
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶员 | |||
女性驾驶员 | |||
合计 |
（2）根据这些样本数据来估计总体，随机调查3辆家庭轿车，记这3辆车中，驾驶员为女性且平均车速不超过的人数为
，假定抽取的结果相互独立，求的分布列和数学期望.
参考公式：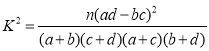
临界值表：
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
