题目内容
8.过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右顶点作x轴的垂线,与C的一条渐近线相交于点A.若以C的右焦点为圆心、半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( )| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
分析 根据圆的性质,求出圆心坐标,即c=4求出A的坐标,代入圆的方程进行求解即可.
解答 解:∵以C的右焦点为圆心、半径为4的圆经过A,O两点(O为坐标原点),
∴半径R=c=4,则圆的标准方程为(x-4)2+y2=16,
A(a,0),y=$\frac{b}{a}•a$=b,即B(a,b),
则(a-4)2+b2=16,
即a2-8a+16+b2=16,
即c2-8a=0,即8a=16,
则a=2,b2=16-4=12,
则双曲线C的方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1,
故选:D
点评 本题主要考查双曲线方程的求解,根据圆的性质先求出半径c=4是解决本题的关键.

练习册系列答案
相关题目
3.已知直线(m+2)x+(m+1)y+1=0上存在点(x,y)满足$\left\{\begin{array}{l}{x+y-3≤0}\\{x-2y-3≤0}\\{x≥1}\end{array}\right.$,则实数m的取值范围是( )
| A. | [-1,$\frac{1}{2}$] | B. | [-$\frac{1}{4}$,$\frac{1}{2}$] | C. | [-$\frac{5}{3}$,+∞) | D. | (-∞,-$\frac{5}{3}$] |
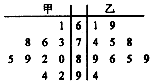 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.