题目内容
求使不等式a3+b3+c3≥3abc成立的实数a,b,c满足的条件.
解：a3+b3+c3-3abc
=(a+b)3-3ab(a+b)+c3-3abc
=(a+b+c)［(a+b)2-(a+b)c+c2］-3ab(a+b+c)
=(a+b+c)［a2+b2+c2-ab-ac-bc］
∵a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac,
∴2(a2+b2+c2)≥2(ab+bc+ca),
∴a2+b2+c2-ab-ac-bc≥0.
故要使a3+b3+c3≥3abc成立,则需a+b+c＞0.
因此当a、b、c∈R+时，a3+b3+c3≥3abc,
当且仅当a=b=c时取等号.
练习册系列答案
相关题目
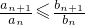对一切n∈N*恒成立，求证：d≤a1q-a1；
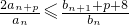成立的自然数n恰有4个的正整数p的值．