题目内容
数列{an}的前n项和为Sn,若a1=2且an+1-2=an.(1)求使不等式Sn<56成立的n的最大值;
(2)是否存在等比数列{bn}满足b1=a1,b2=a3,b3=a9?若存在,则求出数列{bn}的通项公式;若不存在,则说明理由.
【答案】分析:(1)由an-1-2=an,知an-1-an=2,故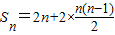 =n2+n.由此能求出使不等式Sn<56成立的n的最大值.
=n2+n.由此能求出使不等式Sn<56成立的n的最大值.
(2)存在存在等比数列{bn}满足b1=a1,b2=a3,b3=a9.由an=2n,知a3=6,a9=18,a1=2,则由b1=a1,b2=a3,b3=a9,由此能推导出存在以b1=2为首项,公比为3的等比数列{bn},其通项公式为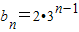 .
.
解答:解:(1)∵an-1-2=an,
∴an-1-an=2,
即数列{an}是以2为首项,公差为2的等差数列,
∴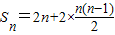
=n2+n.
∴由Sn<56,得0<n<7,n∈N*.
故使不等式Sn<56成立的n的最大值为6.
(2)存在存在等比数列{bn}满足b1=a1,b2=a3,b3=a9.
由(1)知,an=2n,
∴a3=6,a9=18,a1=2,
则由b1=a1,b2=a3,b3=a9,
得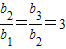 ,
,
即存在以b1=2为首项,公比为3的等比数列{bn},
其通项公式为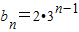 .
.
点评:本题考查等比数列的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性,是高考的重点.解题时要认真审题,仔细解答.
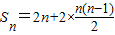 =n2+n.由此能求出使不等式Sn<56成立的n的最大值.
=n2+n.由此能求出使不等式Sn<56成立的n的最大值.(2)存在存在等比数列{bn}满足b1=a1,b2=a3,b3=a9.由an=2n,知a3=6,a9=18,a1=2,则由b1=a1,b2=a3,b3=a9,由此能推导出存在以b1=2为首项,公比为3的等比数列{bn},其通项公式为
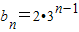 .
.解答:解:(1)∵an-1-2=an,
∴an-1-an=2,
即数列{an}是以2为首项,公差为2的等差数列,
∴
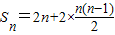
=n2+n.
∴由Sn<56,得0<n<7,n∈N*.
故使不等式Sn<56成立的n的最大值为6.
(2)存在存在等比数列{bn}满足b1=a1,b2=a3,b3=a9.
由(1)知,an=2n,
∴a3=6,a9=18,a1=2,
则由b1=a1,b2=a3,b3=a9,
得
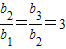 ,
,即存在以b1=2为首项,公比为3的等比数列{bn},
其通项公式为
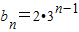 .
.点评:本题考查等比数列的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目