Question

在矩形ABCD中，AB=1，AD=

3

，P为矩形内一点，且AP=

3

2

，若

AP

=λ

AB

+μ

AD

（λ，μ∈R），則λ+

3

μ的最大值为（　　）

• A．

  3

  2

• B．

  3+ 3

  4

• C．

  6

  2

• D．

  6 +3 2

  4

Answer 1

分析：由题意正确得出点P（x，y）所满足的约束条件，利用

AP

=λ

AB

+μ

AD

=（x，y）=λ（1，0）+μ（0，

3

）进行坐标变换得出x，y满足的约束条件，利用基本不等式的方法找出x+y的最大截距即可．

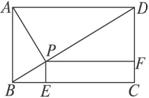
解答：解：如图所示，在图中，设P（x，y）．
B（1，0），D（0，

3

），C（1，

3

）．
由AP=

3

2

，得x²+y²=

3

4

，
则点P满足的约束条件为

0≤x≤1 0≤y≤ 3 x2+y2= 3 4

．
∵

AP

=λ

AB

+μ

AD

即（x，y）=λ（1，0）+μ（0，

3

）
∴x=λ，y=

3

μ，∴λ+

3

μ=x+y．
由于x+y≤

2(x2+y2)

=

2× 3 4

=

6

2

，
当且仅当x=y时取等号．
則λ+

3

μ=x+y的最大值为

6

2

．
故选C．

点评：本题主要考查了向量在几何中的应用，基本不等式的运用，属于中档题．