题目内容
(本题满分12分)在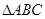
中，已知BC边上的高所在直线的方程为
,
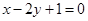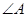平分线所在直线的方程为
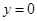，若点B的坐标为（1，2），
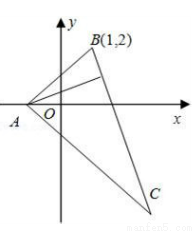
（Ⅰ）求直线BC的方程；
（Ⅱ）求点C的坐标。
【答案】
（Ⅰ）2x+y-4=0（Ⅱ）C（5，-6）
【解析】
试题分析：（Ⅰ）.因为BC与BC边上的高互相垂直，且BC边上的高的斜率为 1/2 ，所以，直线BC的斜率为 -2 ，
因此由点斜式可得直线BC的方程为 y-2=-2(x-1) ，化简得 2x+y-4=0 。
（Ⅱ）由x-2y+1=0和y=0求得A(-1, 0)
由AB，AC关于角A平分线x轴对称的AC直线方程y=-x-1
由 于BC方程为：y=-2x+4 由BC，AC联立解得C（5，-6）
考点：直线方程及直线的位置关系
点评：角的两条边关于角平分线是对称的
练习册系列答案
相关题目
．
，求△ABC的面积．
，0），若实数λ使向量
，λ
，
满足λ2·（
时，过点A1且斜率为1的直线与此时（1）中的曲线相交的另一点为B，能否在直线x=-9上找一点C，使ΔA1BC为正三角形（请说明理由）。
中
分别为A,B,C所对的边，
且
，求
的取值范围
中，数列的前n项和
满足
；（2） 由（1）猜想数列
中，E是BC的中点，F是
的中点
的平面角的余弦值。