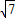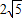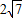题目内容
直线l:ax+y-3a+1=0(a∈R),椭圆C:
+
=1,直线l与椭圆C的公共点的个数为( )
| x2 |
| 25 |
| y2 |
| 36 |
分析:对直线l的方程进行变形,可求得直线所过定点,易判断定点在椭圆内部,从而得到公共点的个数.
解答:解:ax+y-3a+1=0,即a(x-3)+y+1=0,则直线l过定点(3,-1),
又
+
=
+
<1,所以定点(3,-1)在椭圆内部,
故直线l与椭圆有两个公共点,
故选C.
又
| 32 |
| 25 |
| (-1)2 |
| 36 |
| 9 |
| 25 |
| 1 |
| 36 |
故直线l与椭圆有两个公共点,
故选C.
点评:本题考查直线与圆锥曲线的位置关系,根据直线方程正确求出其所过定点是解决本题的关键.

练习册系列答案
相关题目