题目内容
设直线l：ax-y+3=0与圆C：（x-1）2+（y-2）2=9相交于A、B两点，则|AB|的最小值为（ ）A．
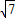
B．
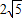
C．
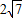
D．6
【答案】分析：运用点到直线的距离公式和基本不等式，算出当且仅当a=1时，圆心C到直线l距离的最大值为2．由此结合垂径定理，即可算出|AB|的最小值．
解答：解：∵圆C：（x-1）2+（y-2）2=9的圆心为（1，2）
∴圆心C到直线l：ax-y+3=0的距离为
d=
=
=2
当且仅当a=1时，d的最大值为2
∵|AB|=
=
∴d取最大值为2时，|AB|有最小值
=
故选：B
点评：本题给出直线与圆相交于A、B两点，求截得弦长的最小值，着重考查了基本不等式、点到直线的距离和用垂径定理求弦长等知识，属于中档题．
解答：解：∵圆C：（x-1）2+（y-2）2=9的圆心为（1，2）
∴圆心C到直线l：ax-y+3=0的距离为
d=
==2当且仅当a=1时，d的最大值为2
∵|AB|=
=∴d取最大值为2时，|AB|有最小值
=故选：B
点评：本题给出直线与圆相交于A、B两点，求截得弦长的最小值，着重考查了基本不等式、点到直线的距离和用垂径定理求弦长等知识，属于中档题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目