题目内容
(本小题满分12分)
已知数列 满足
满足 ,数列
,数列 满足
满足 ,
,
数列 满足
满足 .
.
(1)若 ,证明数列
,证明数列 为等比数列;
为等比数列;
(2)在(1)的条件下,求数列 的通项公式;
的通项公式;
(3)若 ,证明数列
,证明数列 的前
的前 项和
项和 满足
满足 。
。
(1)根据等比数列的定义得到证明。
(2) (3)利用数列求和放缩法得到证明。
(3)利用数列求和放缩法得到证明。
解析试题分析:解:(1)
 ,
,

由已知
 数列
数列 是首项为
是首项为 ,公比为
,公比为 的等比数列;
的等比数列;
(2)由(1)得,


证明(3)首先证明
① 时,
时,
 成立
成立
②假设 时
时 成立
成立
则当 时,
时, 也成立,
也成立,


 ,
,






 ,
,
 ,综上所述:
,综上所述:
考点:本试题主要是考查了数列概念和求和的知识运用。
点评:解决数列的通项公式的求解可以通过定义法或者是递推式来表示得到结论,或者能结合前n项和与其的关系式来求解。对于等比数列的判定,则可以直接运用定义法来说明相邻两项比值为定值来说明,同时要对于有绝对值的数列求和的时候要助于去掉绝对值符号来进行,属于难度试题。

练习册系列答案
相关题目
 的前
的前 项和
项和 ,且满足
,且满足 .
. 的值,猜想
的值,猜想 是数列
是数列 的前
的前 .
. tan x+1=0在x
tan x+1=0在x [0,n
[0,n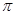 )( n
)( n bn,求实数k的取值范围.
bn,求实数k的取值范围. 的前
的前 项和为
项和为 ,若
,若 ,点
,点 在直线
在直线 上.
上. 是等差数列;
是等差数列; 满足
满足 ,求数列
,求数列 ;
; ,求证:
,求证: .
. 的前n项和
的前n项和 ,且
,且 是
是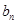 与1的等差中项。
与1的等差中项。 的通项公式;
的通项公式; ,求
,求
 ,是否存在
,是否存在 ,使得
,使得 并说明理由。
并说明理由。 的通项公式为
的通项公式为 ,数列
,数列 的前n项和为
的前n项和为 ,且满足
,且满足
 中是否存在使得
中是否存在使得 是
是 为单调递增的等差数列,
为单调递增的等差数列, ,且
,且 依次成等比数列.
依次成等比数列. ;
; ,求数列
,求数列 的前
的前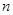 项和
项和 ;
; ,求数列
,求数列 的前
的前 .
. 中,
中, ,
, (
( )
) ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:  .
. 前
前 项和
项和 .数列
.数列 满足
满足
 ,数列
,数列 满足
满足 。(1)求数列
。(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 ;(3)若
;(3)若 对一切正整数
对一切正整数 的取值范围。
的取值范围。