题目内容
已知函数 .
.
(1)求函数 的定义域
的定义域 ,并判断
,并判断 的奇偶性;
的奇偶性;
(2)用定义证明函数 在
在 上是增函数;
上是增函数;
(3)如果当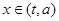 时,函数
时,函数 的值域是
的值域是 ,求
,求 与
与 的值.
的值.
 .
.(1)求函数
 的定义域
的定义域 ,并判断
,并判断 的奇偶性;
的奇偶性;(2)用定义证明函数
 在
在 上是增函数;
上是增函数;(3)如果当
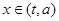 时,函数
时,函数 的值域是
的值域是 ,求
,求 与
与 的值.
的值..解:(1)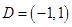 ,函数
,函数 是奇函数.
是奇函数.
(2)设、算、证、结
(3)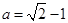 ,
,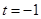
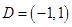 ,函数
,函数 是奇函数.
是奇函数. (2)设、算、证、结
(3)
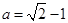 ,
,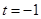
试题分析:
思路分析:(1)由
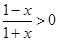 ,求得
,求得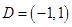
计算
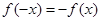 知函数
知函数 是奇函数.
是奇函数. 另证:对任意
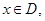
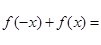 0,
0,(2)利用“定义”“设、算、证、结”。
(3)根据
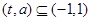 且
且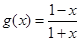 在
在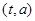 的值域是
的值域是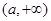 ,
, 得到a的方程
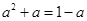 解得
解得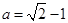 (
( 舍去)
舍去)得到
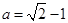 ,
,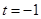 。
。解:(1)令
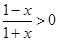 ,解得
,解得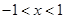 ,
,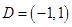
对任意
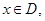
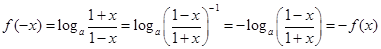
所以函数
 是奇函数.
是奇函数. 另证:对任意
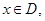
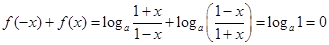 ,
,所以函数
 是奇函数.
是奇函数. (2)设
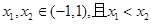 ,
, 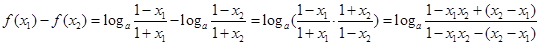
∴
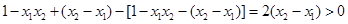
∴
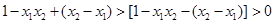
∴
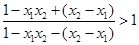 ∵
∵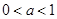 ∴
∴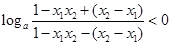
∴
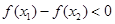 ,∴
,∴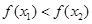
所以函数
 在
在 上是增函数.
上是增函数. (3)由(2)知,函数
 在
在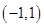 上是增函数,
上是增函数,又因为
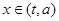 时,
时, 的值域是
的值域是 ,
,所以
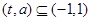 且
且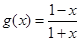 在
在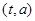 的值域是
的值域是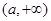 ,
, 故
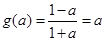 且
且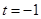 (结合
(结合 图像易得
图像易得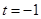 )
)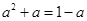 解得
解得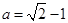 (
( 舍去)
舍去)所以
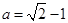 ,
,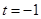
点评:中档题,本题主要考查对数函数的性质,利用函数的奇偶性、单调性定义,判断函数的奇偶性,证明函数的单调性,属于基础题目。

练习册系列答案
相关题目
 的单调区间是
的单调区间是 .
. 有2个零点.
有2个零点. 的图像为曲线C,若曲线C存在与直线
的图像为曲线C,若曲线C存在与直线 垂直的切线,则实数m的取值范围是
垂直的切线,则实数m的取值范围是 .
. 对任意的
对任意的 都有
都有 则实数
则实数 的取值范围是(-
的取值范围是(- ].
]. 长度为
长度为 .已知函数
.已知函数 定义域为
定义域为 ,值域为
,值域为 ,则区间
,则区间 、
、 、
、 ,则
,则 三者的大小关系是( )
三者的大小关系是( )



 ( )
( )



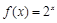 及函数
及函数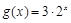 的图象分别相交于A,B两点,则
的图象分别相交于A,B两点,则
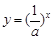 ,当
,当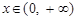 时,有
时,有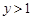 ,解关于x的不等式
,解关于x的不等式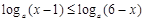
 ,则( )
,则( )

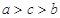

 .
.