题目内容
若f（x）是定义域上的偶函数，且x∈（-∞，-1）时，函数单调递增，那么f（-1），f（2），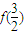
的大小顺序是 ．
【答案】分析：先利用f（x）是定义域上的偶函数得f（2）=f（-2），f（
）=f（-
）．再利用x∈（-∞，-1）时，函数单调递增，两个结论相结合即可求得结论．
解答：解：因为f（x）是定义域上的偶函数
故f（2）=f（-2），f（
）=f（-
）．
∵x∈（-∞，-1）时，函数单调递增且-2＜-
＜-1，
∴f（-2）＜f（-
）＜f（-1）
即f（2）＜f（
）＜f（-1）．
故答案为：f（2）＜f（
）＜f（-1）．
点评：本题主要考查函数的单调性和奇偶性，是对函数基本性质的综合考查，属于基础题．
）=f（-）．再利用x∈（-∞，-1）时，函数单调递增，两个结论相结合即可求得结论．解答：解：因为f（x）是定义域上的偶函数
故f（2）=f（-2），f（
）=f（-）．∵x∈（-∞，-1）时，函数单调递增且-2＜-
＜-1，∴f（-2）＜f（-
）＜f（-1）即f（2）＜f（
）＜f（-1）．故答案为：f（2）＜f（
）＜f（-1）．点评：本题主要考查函数的单调性和奇偶性，是对函数基本性质的综合考查，属于基础题．
练习册系列答案
相关题目
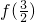的大小顺序是________．
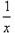-ax2+x（a＞0），