��Ŀ����
��ͼ,��ƽ��ֱ������ϵxOy��,��֪��ԲE: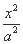 +
+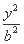 =1(a>b>0)��������e=
=1(a>b>0)��������e=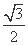 ,A1,A2�ֱ�����ԲE��������������,ԲA2�İ뾶Ϊa,����A1��ԲA2������,�е�ΪP,��x����Ϸ�����ԲE�ڵ�Q.
,A1,A2�ֱ�����ԲE��������������,ԲA2�İ뾶Ϊa,����A1��ԲA2������,�е�ΪP,��x����Ϸ�����ԲE�ڵ�Q.
(1) ��ֱ��OP�ķ���;
(2) �� ��ֵ;
��ֵ;
(3) ��aΪ����,����O���������ഹֱ��ֱ��,�ֱ���ԲE�ڵ�B,C,�ֱ�ԲA2�ڵ�M,N,��OBC��OMN������ֱ�ΪS1,S2,��S1��S2�����ֵ.
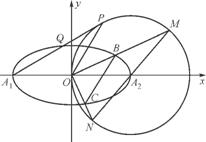
(1) ����A2P,��A2P��A1P,��A2P=a.
��A1A2=2a,���ԡ�A1A2P=60��.
���ԡ�POA2=60��,����ֱ��OP�ķ���Ϊy= x.
x.
(2) ��(1)֪,ֱ��A2P�ķ���Ϊy=- (x-a),A1P�ķ���Ϊy=
(x-a),A1P�ķ���Ϊy= (x+a),
(x+a),
�������xP= .
.
��Ϊe=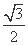 ,��
,�� =
=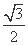 ,����c2=
,����c2= a2,b2=
a2,b2= a2,����ԲE�ķ���Ϊ
a2,����ԲE�ķ���Ϊ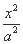 +
+ =1.
=1.
�� ���xQ=-
���xQ=- ,
,
���� =
= =
= .
.
(3) ������OM�ķ���Ϊy=kx(k>0),
����������
���B ,
,
����OB=a .
.
��- ���������k,��OC=a
���������k,��OC=a .
.
ͬ���ɵ�,OM= ,ON=
,ON= .
.
����S1��S2= ��OB��OC��OM��ON=a4��
��OB��OC��OM��ON=a4�� .
.
��Ϊ =
= ��
�� ,
,
���ҽ���k=1ʱ�Ⱥų���,����S1��S2�����ֵΪ .
.

��ϰ��ϵ�д�
�����Ŀ
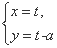 (tΪ����)����ԲC:
(tΪ����)����ԲC: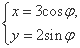 (��Ϊ����)���Ҷ���,����a��ֵ.
(��Ϊ����)���Ҷ���,����a��ֵ.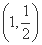 ��Բx2+y2=1������,�е�ֱ�ΪA,B,ֱ��ABǡ�þ�����Բ���ҽ�����϶���,����Բ�ķ����ǡ�����������.
��Բx2+y2=1������,�е�ֱ�ΪA,B,ֱ��ABǡ�þ�����Բ���ҽ�����϶���,����Բ�ķ����ǡ�����������.  }��N��{x|x�ܣ�1}��P��{x|x��
}��N��{x|x�ܣ�1}��P��{x|x��