题目内容
“tanx=﹣1”是“x=﹣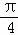
+2kπ（k∈Z）”的（ ）
A． 充分非必要条件 B． 必要非充分条件 C． 充要条件 D． 既非充分又非必要条件
B
考点： 函数奇偶性的性质．
专题： 简易逻辑．
分析： 得出tan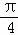（=﹣+2kπ）=﹣1，“x=﹣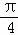+2kπ”是“tanx=﹣1”成立的充分条件；举反例tan
=﹣1，推出“x=﹣
+2kπ（k∈Z）”是“tanx=﹣1”成立的不必要条件．
解答： 解：tan（﹣+2kπ）=tan （﹣）=﹣1，所以充分；但反之不成立，如tan =﹣1．
练习册系列答案
金钥匙试卷系列答案
相关题目
，且α＝a＋
，β＝b＋
，则α＋β的最小值为( )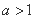
”是“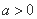
” 的………………………………………………………………（ ）
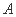）充分非必要条件 （
）必要非充分条件 
）充要条件 （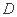
）既非充分又非必要条件 
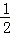，求正四棱柱ABCD﹣A1B1C1D1的体积．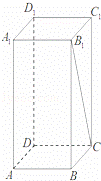
的解是 ___________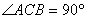
，E为BB1中点，
，
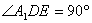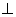平面A1ABB1；
棱锥A1—CDE的体积。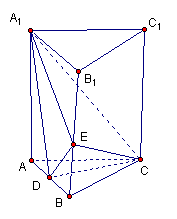
中，
，点
在棱
上移动，
； （2）当
的距离；
为何值时，二面角
的大小为
．