题目内容
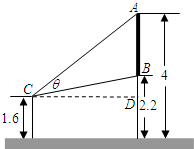 如图,有一壁画,最高点A 处离地面4 m,最低点B 处离地面2.2 m,若从离地高1.6 m的C 处观赏它,则当视角θ 最大时,C 处离开墙壁
如图,有一壁画,最高点A 处离地面4 m,最低点B 处离地面2.2 m,若从离地高1.6 m的C 处观赏它,则当视角θ 最大时,C 处离开墙壁1.2
1.2
m.分析:作CD⊥AB,交AB于D,设当视角θ 最大时,C 处离墙xm远,tan∠ACD=
,tan∠BCD=
,视角θ=∠ACD-∠BCD,tanθ=tan(∠ACD-∠BCD)=
=
=
≤
=
.由此能求出结果.
| 2.4 |
| x |
| 0.6 |
| x |
| ||||
1+
|
| ||
1+
|
| 1.8x |
| x2+1.44 |
| 1.8x | ||
2
|
| 3 |
| 4 |
解答:解:作CD⊥AB,交AB于D,当视角θ 最大时,C处设离墙xm远
tan∠ACD=
=
,
tan∠BCD=
=
,
视角θ=∠ACD-∠BCD,
tanθ=tan(∠ACD-∠BCD)
=
=
=
=
≤
=
=
.
当且仅当x2=1.44,x>0,即x=1.2m时,取最大值.
故答案为:1.2.
tan∠ACD=
| 4-1.6 |
| x |
| 2.4 |
| x |
tan∠BCD=
| 2.2-1.6 |
| x |
| 0.6 |
| x |
视角θ=∠ACD-∠BCD,
tanθ=tan(∠ACD-∠BCD)
=
| tan∠ACD-tan∠BCD |
| 1+tan∠ACD•tan∠BCD |
=
| ||||
1+
|
=
| ||
1+
|
=
| 1.8x |
| x2+1.44 |
≤
| 1.8x | ||
2
|
=
| 1.8x |
| 2.4x |
=
| 3 |
| 4 |
当且仅当x2=1.44,x>0,即x=1.2m时,取最大值.
故答案为:1.2.
点评:本题考查解三角形在生产实际中的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,容易出错.解题时要注意正切加法定理和数形结合思想的灵活运用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
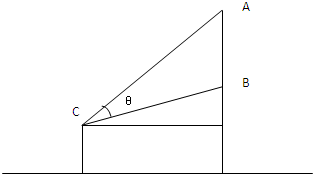 如图,有一壁画,最高点A处离地面4m,最低点B处离地面2m.若从地面高1.5m的C处观赏它,则离墙多远时,视角θ最大.
如图,有一壁画,最高点A处离地面4m,最低点B处离地面2m.若从地面高1.5m的C处观赏它,则离墙多远时,视角θ最大.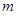 ,最低点B处离地面2
,最低点B处离地面2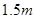 的C处观赏它,则离墙多远的视角
的C处观赏它,则离墙多远的视角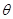 最大?
最大?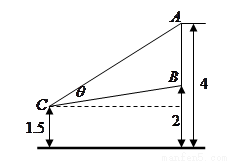
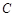 处观赏它,则
处观赏它,则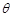 最大?
最大?
 处观赏它,则离墙多远时,视角
处观赏它,则离墙多远时,视角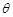 最大?
最大?