题目内容
已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12.
(1)试证明:不论k为何实数,直线l和圆C总有两个交点;
(2)求直线l被圆C截得的最短弦长.
(1)见解析;(2)
【解析】试题解析:(1)因为不论k为何实数,直线l总过点A(1,0),而 ,所以点A在圆C的内部,即不论k为何实数,直线l和圆C总有两个交点
,所以点A在圆C的内部,即不论k为何实数,直线l和圆C总有两个交点
(2)由几何性质过点A(1,0)的弦只有和AC垂直时最短,而此时点A(1,0)为弦的中点,由勾股定理,弦长为 ,
,
考点:本题考查直线与圆的位置关系

练习册系列答案
相关题目
 的图象在点
的图象在点 处的切线的斜率为2.
处的切线的斜率为2. 的值;
的值; ,讨论
,讨论 的单调性;
的单调性; 且
且 ,证明:
,证明:
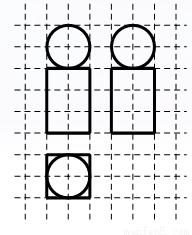
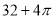 (B)
(B)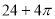 (C)
(C) (D)
(D)
 与双曲线
与双曲线 的一条渐近线的交点(异于原点),若点A到抛物线
的一条渐近线的交点(异于原点),若点A到抛物线 的准线的距离为
的准线的距离为 ,则双曲线
,则双曲线 的离心率等于( )
的离心率等于( ) B.2 C.
B.2 C. D.4
D.4 满足
满足 ,则
,则 ( )
( ) D.
D.
 中,
中, ,公差为
,公差为 ,前
,前 项和为
项和为 ,当且仅当
,当且仅当 时
时 满足
满足 ,
, ,
, =2,则
=2,则 =( )
=( ) C.
C. D.2
D.2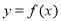 的周期为2,当
的周期为2,当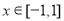 时
时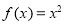 ,那么函数
,那么函数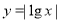 的图象的交点共有( )
的图象的交点共有( )