题目内容
已知f(x)=(1)求f(x)的定义域;
(2)若α∈(0,![]() )且cos(
)且cos(![]() -α)=
-α)=![]() ,求f(α)的值.
,求f(α)的值.
解:(1)tanx的定义域是{x|x≠![]() +kπ,k∈Z}.
+kπ,k∈Z}.
又由1+tanx≠0,得x≠![]() +kπ,k∈Z.故f(x)的定义域是{x|x≠
+kπ,k∈Z.故f(x)的定义域是{x|x≠![]() +kπ且x≠
+kπ且x≠![]() +kπ,k∈Z}.
+kπ,k∈Z}.
(2)方法一:f(α)=![]()
=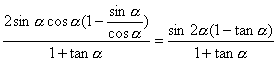
=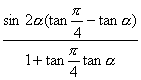 =sin2αtan(
=sin2αtan(![]() -α).
-α).
∵α∈(0,![]() ),-α∈(
),-α∈(![]() ,0),
,0),![]() -α∈(0,
-α∈(0,![]() ),∴sin(
),∴sin(![]() -α)=
-α)=![]() .
.
∴tan(![]() -α)=
-α)=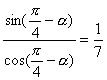 .
.
∵cos[2(![]() -α)]=cos(
-α)]=cos(![]() -2α)=sin2α,
-2α)=sin2α,
又cos[2(![]() -α)]=2cos2(
-α)]=2cos2(![]() -α)-1=2×
-α)-1=2×![]() ,
,
∴f(α)=![]() .
.
方法二:由cos(![]() -α)=
-α)=![]() (cosα+sinα)=
(cosα+sinα)=![]() ,
,
∴cosα+sinα=![]() .由
.由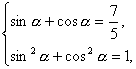
解得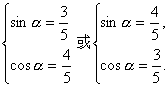
∵α∈(0,![]() ),故cosα>sinα.∴cosα=
),故cosα>sinα.∴cosα=![]() ,sinα=
,sinα=![]() .
.
于是tanα=![]() =
=![]() .
.
又sin2α=2sinαcosα=![]() .
.
∴f(α)=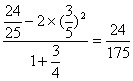 .
.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目