题目内容
 如图在一个圆心角为2弧度,半径为2的扇形内有一个边长为1的正方形,若向扇形内任投一点,则该点落在正方形内的概率为________.
如图在一个圆心角为2弧度,半径为2的扇形内有一个边长为1的正方形,若向扇形内任投一点,则该点落在正方形内的概率为________.

分析:本题是一个几何概率模型,向扇形内任投一点,则该点落在正方形内的概率为正方形的面积与扇形面积的比值.因此运用公式求出扇形的面积和正方形的面积,本题的概率即可求出.
解答:∵扇形的圆心角为2弧度,半径为R=2
∴扇形的弧长为L=2×2=4
可得扇形的面积为S=
 =4
=4又∵正方形边长为1
∴正方形面积为S1=12=1
因此向扇形内任投一点,则该点落在正方形内的概率为
P=
 =
=
点评:本题考查了几何概型,着重考查了扇形的弧长公式和面积公式,属于基础题.几何概型的算法往往是用符合题意图形的面积(体积或长度等)除以整个图形的面积(体积或长度等).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
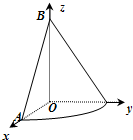 如图,直角三角形OAB的直角顶点O是空间坐标系O-xyz的原点,点A在Ox轴正半轴上,|OA|=1;点B在Oz轴正半轴上,|OB|=2.我们称△OAB绕Oz轴逆时针旋转
如图,直角三角形OAB的直角顶点O是空间坐标系O-xyz的原点,点A在Ox轴正半轴上,|OA|=1;点B在Oz轴正半轴上,|OB|=2.我们称△OAB绕Oz轴逆时针旋转| π |
| 2 |
| A、该四分之一圆锥体主视图和左视图的图形是全等的直角三角形 | ||
B、该四分之一圆锥体俯视图的图形是一个圆心角为
| ||
| C、该四分之一圆锥体主视图、左视图和俯视图的图形都是扇形 | ||
| D、该四分之一圆锥体主视图的图形面积大于俯视图的图形面积 |
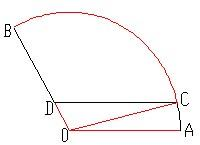 如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为
如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为 如图在一个圆心角为2弧度,半径为2的扇形内有一个边长为1的正方形,若向扇形内任投一点,则该点落在正方形内的概率为
如图在一个圆心角为2弧度,半径为2的扇形内有一个边长为1的正方形,若向扇形内任投一点,则该点落在正方形内的概率为