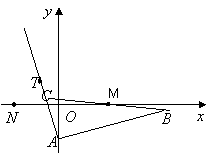
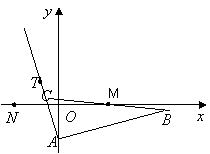
题目内容
已知![]() 的边
的边![]() 边所在直线的方程为
边所在直线的方程为![]()
点B关于点![]() 的对称点为C, 点
的对称点为C, 点![]() 在AC边所在直线上且满足
在AC边所在直线上且满足![]() .
.
(I)求AC边所在直线的方程;
(II)求![]() 的外接圆的方程;
的外接圆的方程;
(III)若点N的坐标为![]() 其中n为正整数。试讨论在
其中n为正整数。试讨论在![]() 的外接圆上是否存在点P,使得
的外接圆上是否存在点P,使得![]() 成立?说明理由。
成立?说明理由。
 |
.解:(I)![]()
![]()
![]() , ………………..1分
, ………………..1分
又![]() 边所在直线的方程为
边所在直线的方程为![]() ,,所以直线AC的斜率为
,,所以直线AC的斜率为![]() .……2分
.……2分
又因为点![]() 在直线AC上,
在直线AC上,
所以AC边所在直线的方程为![]() .即
.即![]() . …………3分
. …………3分
(II)AC与AB的交点为A,所以由![]() 解得点
解得点![]() 的坐标为
的坐标为![]() ,…5分
,…5分
![]() …………6分
…………6分
又r=![]() . …………7分
. …………7分
从![]() 外接圆的方程为:
外接圆的方程为: ![]() . …………8分
. …………8分
(III)若在![]() 的外接圆圆M上存在点P,使得
的外接圆圆M上存在点P,使得![]() 成立,则P为线段NT的垂直平分线L与圆M的公共点。所以当L与圆M相离时,不存在满足条件的点P;当L与圆M相交或相切时则存在满足条件的点P。
成立,则P为线段NT的垂直平分线L与圆M的公共点。所以当L与圆M相离时,不存在满足条件的点P;当L与圆M相交或相切时则存在满足条件的点P。
由N![]()
![]() ,知NT的斜率为
,知NT的斜率为![]() ,线段NT的中点为
,线段NT的中点为![]()
线段NT的垂直平分线L为![]()
………10分
圆M的圆心M到直线L的距离为
d=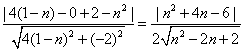 …………11分
…………11分
i)当n=1时,d=![]() ,此时直线L与圆M相交,存在满足条件的点P
,此时直线L与圆M相交,存在满足条件的点P
ii)当n=2时 d=![]() ,此时直线L与圆M相交,存在满足条件的点P
,此时直线L与圆M相交,存在满足条件的点P
iii)当![]() 时,
时,
![]()
此时直线L与圆M相离,不存在满足条件的点P。 …………14分
(说明:(III) 求出NT的垂直平分线,与圆M方程联立方程组,消元得二次方程后提到用判别式讨论的即可得3分; 用图形说明当n增大时M到L的距离d也增大,当n=3时有d>r,所以n>3时有d>r,只扣1分)

 已知
已知 已知
已知