题目内容
已知点 ,点
,点 为直线
为直线 上的一个动点.
上的一个动点.
(Ⅰ)求证: 恒为锐角;
恒为锐角;
(Ⅱ)若四边形 为菱形,求
为菱形,求 的值.
的值.
(Ⅰ)证明见解析;(Ⅱ)2.
解析试题分析:(Ⅰ)已知一个角的两边的向量,可以求出这个角的大小,由题,可以求出向量PA,PB,由向量内积公式可求得角的范围;(Ⅱ)菱形的对边平行且四边相等,向量相等,横纵坐标相等,由题,向量AP=BP,可以求得x=1,由向量PQ=BA,可以求得Q点坐标,即可求出向量的内积.
试题解析:(Ⅰ)∵点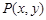 在直线
在直线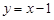 上,
上,
∴点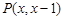 ,
,
∴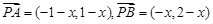 ,
,
∴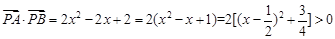 ,
,
∴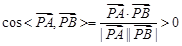 ,
,
若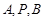 三点在一条直线上,则
三点在一条直线上,则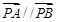 ,
,
得到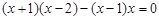 ,方程无解,
,方程无解,
∴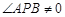 ,
,
∴ 恒为锐角.
恒为锐角.
(Ⅱ)∵四边形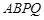 为菱形,
为菱形,
∴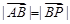 ,即
,即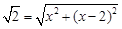
化简得到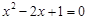 ,
,
∴ ,
,
∴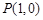 ,
,
设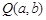 ,∵
,∵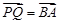 ,
,
∴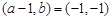 ,
,
∴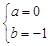 ,
,
∴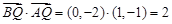 .
.
考点:1.用向量的内积求角;2.菱形.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 b,且|c|
b,且|c| 1,a
1,a (b-c)=0,则实数
(b-c)=0,则实数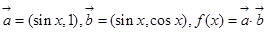
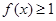 ,求x的范围;
,求x的范围;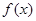 的最大值以及此时x的值.
的最大值以及此时x的值. ,
, 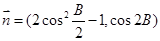 ,且
,且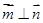 ,
,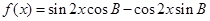 的单调减区间;
的单调减区间;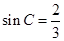 ,求
,求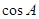 .
. .
. ,求
,求 的坐标;
的坐标; ,若
,若 ,求
,求 点坐标.
点坐标. ,点
,点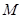 为
为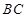 的中点,点
的中点,点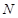 满足
满足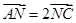 ,点
,点 满足
满足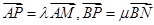 .
.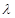 与
与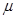 的值;
的值; 三点坐标分别为
三点坐标分别为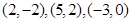 ,求
,求 ,
, ,
, ,
, 为坐标原点.
为坐标原点. ,求
,求 的值;;
的值;; ,且
,且 ,求
,求 与
与 的夹角.
的夹角. 与
与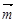 =(1,1)共线。
=(1,1)共线。 或x>
或x>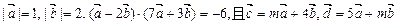 ,
,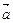 和
和 的夹角;
的夹角;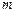 取何值时,
取何值时,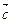 与
与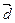 共线?
共线?