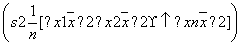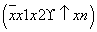题目内容
如图,直四棱柱ABCD—A1B1C1D1的底面ABCD为平行四边形,其中AB=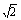 ,BD=BC=1,AA1=2,E为DC中点,点F在DD1上,且DF=
,BD=BC=1,AA1=2,E为DC中点,点F在DD1上,且DF=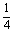 。
。
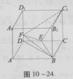
(1)求异面直线BD与A1D1的距离;
(2)EF与BC1是否垂直?请说明理由;
(3)求二面角E—FB—D的正切值。

 同正解一;
同正解一;
 由已知可得∠ADB=90°,DD1⊥平面ABCD,∴以
由已知可得∠ADB=90°,DD1⊥平面ABCD,∴以 、
、 、
、 分别为x,轴y轴,z轴的正方向,建立空间坐标系,F(0,0,
分别为x,轴y轴,z轴的正方向,建立空间坐标系,F(0,0,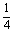 )、E(
)、E( )、A(1,0,0)、D1(0,0,2),∴
)、A(1,0,0)、D1(0,0,2),∴ =
=
 =(-1,0,2)
=(-1,0,2) 又BC1∥AD1,∴EF⊥AD1。
又BC1∥AD1,∴EF⊥AD1。
 可以得平面BDF的一个法向量为
可以得平面BDF的一个法向量为 =(-1,0,0),B(0,1,0)
=(-1,0,0),B(0,1,0) ,设平面BEF的一个法向量为n=(x,y,z)由n⊥
,设平面BEF的一个法向量为n=(x,y,z)由n⊥ ,令x=1,得y=-1,z=-4, ∴平面BEF的一个法向量为n=(1,-1,-4),∴cosα=
,令x=1,得y=-1,z=-4, ∴平面BEF的一个法向量为n=(1,-1,-4),∴cosα= ,∴所求二面角E—FB—D的大小为arccos
,∴所求二面角E—FB—D的大小为arccos

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
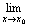 f(x)存在是函数f(x)在点x=x0处连续的 ( )
f(x)存在是函数f(x)在点x=x0处连续的 ( ) 是直线
是直线 上的动点,
上的动点, 是圆
是圆 的切线,
的切线, 是切点,
是切点,  是圆心,那么四边形
是圆心,那么四边形 面积的最小值是( ).
面积的最小值是( ).  B.
B. C.
C. D.
D.
 ,且在y轴上的截距是在x轴上的截距的2倍的直线方程是 ( )
,且在y轴上的截距是在x轴上的截距的2倍的直线方程是 ( ) B.
B.


 棱长为4的正方体ABCD—A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP。
棱长为4的正方体ABCD—A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP。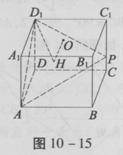
 的斜线段,A为斜足,若点P在平面
的斜线段,A为斜足,若点P在平面
 线 D.两条平行直线
线 D.两条平行直线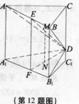
 1D的距离;
1D的距离;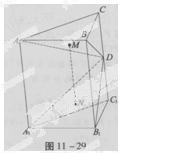
 C.60° D.90°
C.60° D.90°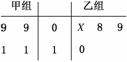
 同学,求这两名同学的植树总棵数为19的概率.
同学,求这两名同学的植树总棵数为19的概率.