Question

【题目】设数列 的前 n 项和为 Sn ，且(3-m)Sn+2man=m+3() ，其中 m 为常数，且 .
①求证： 是等比数列；
②若数列 的公比为q=f(m) ，数列 {bn} 满足 b1=a1 ， ，求证： 为等差数列.

Answer 1

【答案】【解答】解：①由 (3-m)Sn+2man=m+3 ，得(3-m)Sn+1+2man+1=m+3 ，
两式相减，得(3+m)an+1=2man ( ) ，
∴ .
又m为常数，且 ，∴ 是等比数列.
②∵ (3-m)Sn+2man=m+3 ，
∴(3-m)a1+2ma1=m+3 .
∴ a1=1,b1=a=1, .
由①可得， .
∴ 当 ，且 时， .∴ .
∴ .
∴数列 是首项为1，公差为 的等差数列.
【解析】本题主要考查了分析法与综合法，解决问题的关键是需要利用等比数列、等差数列的定义使用综合法加以证明，解题的关键是恰当地处理递推关系.
综合法证明数列问题时的证明依据主要来源于以下数列的相关知识：(1)数列的概念，特别是等差数列、等比数列的定义；(2)等差数列与等比数列的基本性质以及数列前 n 项和的性质；(3)数列的通项公式 an 与数列的前 n 项和 Sn 之间的关系 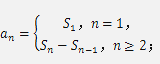(4)递推公式与通项公式的关系.