题目内容
若定义在R上的函数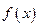 对任意的
对任意的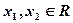 ,都有
,都有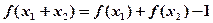 成立,且当
成立,且当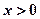 时,
时, 。
。
(1)求证: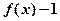 为奇函数; (2)求证:
为奇函数; (2)求证: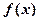 是R上的增函数;
是R上的增函数;
(3)若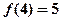 ,解不等式
,解不等式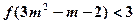 .
.
解:(1)证明:定义在R上的函数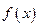 对任意的
对任意的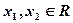 ,
,
都有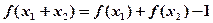 成立
成立
令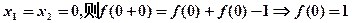 (1分)
(1分)
令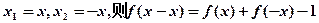
∴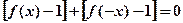 (3分)
(3分)
∴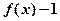 为奇函数 (4分)
为奇函数 (4分)
(2)证明:由(1)知: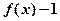 为奇函数, ∴
为奇函数, ∴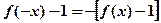 (5分)
(5分)
任取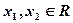 ,且
,且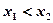 ,则
,则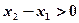
∵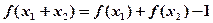
∴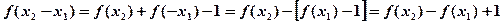
∵当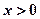 时,
时, ,
,
∴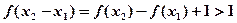 ,∴
,∴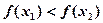 (8分)
(8分)
∴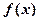 是R上的增函数。 (9分)
是R上的增函数。 (9分)
(3)解:∵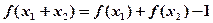 ,且
,且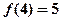
∴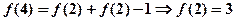 (10分)
(10分)
由不等式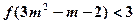 ,得
,得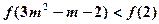 (11分)
(11分)
由(2)知: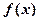 是R上的增函数
是R上的增函数
∴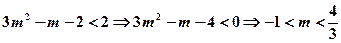 (13分)
(13分)
∴不等式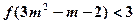 的解集为:
的解集为: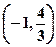
解析

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
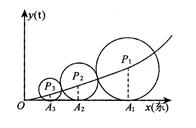
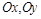 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线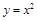 的一段,在小道上依次以点
的一段,在小道上依次以点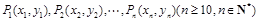 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道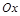 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若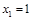 (单位:百米)且
(单位:百米)且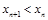 .
.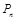 为圆心的圆与主干道
为圆心的圆与主干道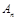 点,证明:数列
点,证明:数列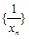 是等差数列,并求
是等差数列,并求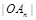 关于
关于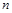 的表达式;
的表达式;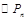 的面积为
的面积为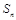 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为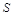 的圆型小道的施工工时为
的圆型小道的施工工时为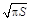 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量 (万件)与月份
(万件)与月份 .
. (万件)与月份
(万件)与月份
 是定义在R上的奇函数,且对任意a、b
是定义在R上的奇函数,且对任意a、b ,当
,当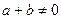 时,都有
时,都有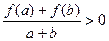 .
.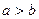 ,试比较
,试比较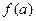 与
与 的大小关系;
的大小关系;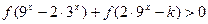 对任意
对任意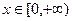 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. 年每件小包的生产成本
年每件小包的生产成本 元,若皮制产品的销售价格不变,第
元,若皮制产品的销售价格不变,第 万元(今年为第一年).
万元(今年为第一年).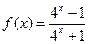 (1)解不等式
(1)解不等式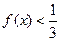 ; (2)求函数
; (2)求函数 的值域.
的值域.
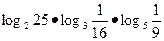 .
.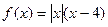 的图象并指出单调区间;
的图象并指出单调区间;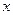 方程
方程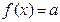 (
(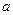 为常数)解的个数?
为常数)解的个数?