题目内容
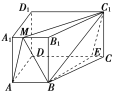
【题目】记边长为1的正六边形的六个顶点分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,集合
,集合![]() ,在
,在![]() 中任取两个元素
中任取两个元素![]() 、
、![]() ,则
,则![]() 的概率为________
的概率为________
【答案】![]()
【解析】
先以![]() 的中点为坐标原点
的中点为坐标原点![]() ,以
,以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 的垂直平分线为
的垂直平分线为![]() 轴,建立平面直角坐标系,得到各顶点坐标,列举出集合
轴,建立平面直角坐标系,得到各顶点坐标,列举出集合![]() 中所有元素,以及满足条件的组合,根据古典概型的概率计算公式,即可求出结果.
中所有元素,以及满足条件的组合,根据古典概型的概率计算公式,即可求出结果.
以![]() 的中点为坐标原点
的中点为坐标原点![]() ,以
,以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 的垂直平分线为
的垂直平分线为![]() 轴,建立如图所示的平面直角坐标系,
轴,建立如图所示的平面直角坐标系,

因为正六边形的边长为![]() ,
,
所以易得:![]() 、
、![]() 、
、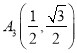 、
、![]() 、
、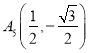 、
、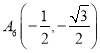 ,
,
因此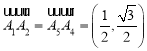 ,
,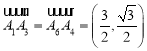 ,
,![]() ,
,![]() ,
,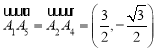 ,
,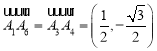 ,
,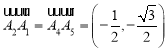 ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,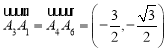 ,
,![]() ,
,![]() ,
,![]() ,
,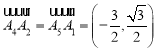 ,
,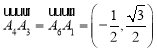 ,
,![]() ;
;
共![]() 个向量.
个向量.
因此![]() 中含有
中含有![]() 个不同的元素.
个不同的元素.
又在![]() 中任取两个元素
中任取两个元素![]() 、
、![]() ,满足
,满足![]() 的有:
的有: 与
与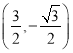 或
或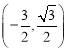 ;
;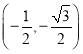 与
与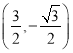 或
或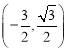 ;
; 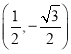 与
与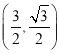 或
或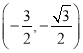 ;
;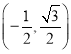 与
与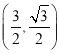 或
或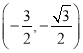 ;
;![]() 与
与![]() 或
或![]() ;
;![]() 与
与![]() 或
或![]() ;
; ![]() 与
与![]() 或
或![]() ;
;![]() 与
与![]() 或
或![]() ;
;![]() 与
与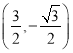 或
或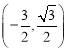 ;
;![]() 与
与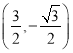 或
或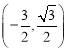 ;
;![]() 与
与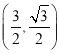 或
或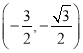 ;
;![]() 与
与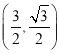 或
或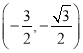 ;共
;共![]() 种选法,又由
种选法,又由![]() 、
、![]() 的任意性,因此满足
的任意性,因此满足![]() 的情况共有:
的情况共有:![]() 种;
种;
又在![]() 中任取两个元素
中任取两个元素![]() 、
、![]() ,共有
,共有![]() 种情况;
种情况;
因此,满足![]() 的概率为:
的概率为:![]() .
.
故答案为:![]()

练习册系列答案
相关题目