题目内容
设
,
是两个非零向量,给出下面四个结论:
①若|
+
|=|
|-|
|,则
⊥
;
②若
⊥
,则|
+
|=|
|-|
|;
③若|
+
|=|
|-|
|,则存在实数λ,使得
=λ
;
④若存在实数λ,使得
=λ
,则|
+
|=|
|-|
|.
其中正确结论的序号是
| a |
| b |
①若|
| a |
| b |
| a |
| b |
| a |
| b |
②若
| a |
| b |
| a |
| b |
| a |
| b |
③若|
| a |
| b |
| a |
| b |
| b |
| a |
④若存在实数λ,使得
| b |
| a |
| a |
| b |
| a |
| b |
其中正确结论的序号是
③
③
.(把你认为正确的序号都填上)分析:本题可以根据选项逐个进行排除,也可以根据向量模的几何意义利用数形结合思想进行分析,或者将模的运算转化为数量积的形式进行分析.
解答:解:①中,若
=-
,则等式|
+
|=|
|-|
|成立,显然
⊥
不成立;
②中,若
⊥
且|
|=|
|,则|
|-|
|=0,显然,|
+
|=
|
|≠0,故|
+
|=|
|-|
|不成立;
④中,若
=
,则|
|-|
|=0,显然,|
+
|=2|
|≠0,故|
+
|=|
|-|
|不成立,
综上,①②④都不正确,
故答案为:③.
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
②中,若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 2 |
| a |
| a |
| b |
| a |
| b |
④中,若
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
综上,①②④都不正确,
故答案为:③.
点评:本题考查平面向量数量积的性质及其运算,属基础题.

练习册系列答案
相关题目
 ,
, 是两个非零向量,则“向量
是两个非零向量,则“向量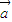 ,
,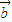 是两个非零向量,则“向量
是两个非零向量,则“向量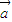 ,
,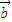 的夹角为锐角”是“函数f(x)=(x
的夹角为锐角”是“函数f(x)=(x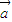 +
+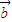 )•(
)•(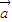 -x
-x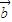 )的图象是一条开口向下的抛物线”的( )
)的图象是一条开口向下的抛物线”的( )