题目内容
【题目】如图，在平面直角坐标系xOy中，已知椭圆 
+ 
=1（a＞b＞0）的离心率为 
，C为椭圆上位于第一象限内的一点．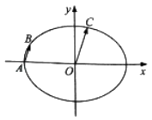
（1）若点C的坐标为（2， 
），求a，b的值；
（2）设A为椭圆的左顶点，B为椭圆上一点，且 
= 
，求直线AB的斜率．
【答案】
（1）解：由题意可知：椭圆的离心率e= 
= 
= 
，则 
= 
，①
由点C在椭圆上，将（2， 
）代入椭圆方程， 
，②
解得：a2=9，b2=5，
∴a=3，b= 
，
（2）方法一：由（1）可知： = ，则椭圆方程：5x2+9y2=5a2，
设直线OC的方程为x=my（m＞0），B（x1，y1），C（x2，y2），
，消去x整理得：5m2y2+9y2=5a2，
∴y2= 
，由y2＞0，则y2= 
，
由 
= 
，则AB∥OC，设直线AB的方程为x=my﹣a，
则 
，整理得：（5m2+9）y2﹣10amy=0，
由y=0，或y1= 
，
由 = ，则（x1+a，y1）=（ 
x2， y2），
则y2=2y1，
则 =2× ，（m＞0），
解得：m= 
，
则直线AB的斜率 
= 
；
方法二：由（1）可知：椭圆方程5x2+9y2=5a2，则A（﹣a，0），
B（x1，y1），C（x2，y2），
由 = ，则（x1+a，y1）=（ x2， y2），则y2=2y1，
由B，C在椭圆上，
∴ 
，解得： 
，
则直线直线AB的斜率k= 
= ．
直线AB的斜率 ．
【解析】（1）根据离心率表示出
，根据点C在椭圆上，代入即可得到a，b的值，（2）方法一：根据（1）得到椭圆方程，设直线OC的方程为x=my（m＞0），B（x1，y1），C（x2，y2），联立方程利用韦达定理可解出m的值，方法二：根据（1）得到椭圆方程，则A（﹣a，0），
B（x1，y1），C（x2，y2），由向量关系和B、C在椭圆上，解出x2，y2，可得直线AB的斜率.
